
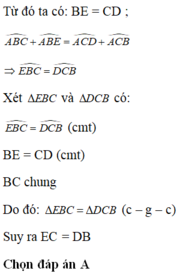
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


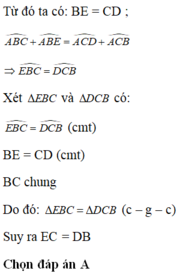

cái thể loại 0 điểm hỏi đáp , đăng toán hình mà éo vẽ hình không = rác rưởi

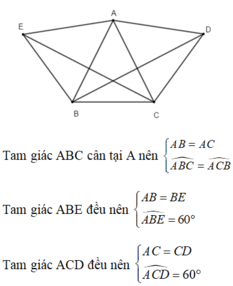
Vì \(\Delta ABC\) cân tại A nên AB=AC (đ/n) và \(\widehat{ABC}=\widehat{ACB}\)
Xét \(\Delta EBC\) và \(\Delta DCB\) có :
\(\widehat{EBC}=\widehat{DCB}\)
BC chung
\(\widehat{BEC}=\widehat{CDB}\) (=90o)
=> \(\Delta EBC\)=\(\Delta DCB\)(cgv-gnk)
=> BD=CE( cctư) (đpcm)
b) Vì \(\Delta EBC\)=\(\Delta DCB\)nên \(\widehat{IBC}=\widehat{ICB}\)(cgtư)
Xét\(\Delta IBC\)Có :\(\widehat{IBC}=\widehat{ICB}\)=> \(\Delta IBC\)cân=> IB=IC(đ/n)
c) Gọi giao điểm của AI và BC là O
Vì \(\widehat{ABC}=\widehat{ACB}\) và \(\widehat{IBC}=\widehat{ICB}\) nên \(\widehat{ABI}=\widehat{ACI}\)
Xét \(\Delta ABI\) và \(\Delta ACI\) có :
AB=AC
\(\widehat{ABI}=\widehat{ACI}\)
IB=IC
=> \(\Delta ABI=\Delta ACI\left(c.g.c\right)\)
=> \(\widehat{BAI}=\widehat{CAI}\left(cgtư\right)\)
Xét \(\Delta ABO\) và \(\Delta ACO\) có :
AB=AC
\(\widehat{ABO}=\widehat{ACO}\)
\(\widehat{BAO}=\widehat{CAO}\)
=> \(\Delta ABO=\Delta ACO\left(c.g.c\right)\)
=> \(\widehat{BOA}=\widehat{COA}\left(cgtư\right)\)
mà \(\widehat{BOA}+\widehat{COA}=180^o\)
=> \(\widehat{BOA}=\widehat{COA}\left(=90^o\right)\)
hay AI\(\perp\)BC (đpcm)

E C B A D I
A)Xét tam giác ADB và tam giác AEC có
\(\widehat{AEC}=\widehat{ADB=90}^0\left(GT\right)\)
\(AB=AC\left(GT\right)\)
\(\widehat{A}chung\)
Từ ba điều trên => tam giác ABD= tam giác AEC( G.C.G)
=> BD=CE( 2 CẠNH T/Ư)
B) Xét tam giác AED, có: \(AE=AD\)(tam giác ADB= tam giác AEC)
=> Tam giác AED là tam giác cân
C) câu c) mk chư bt lm
c ) +)Xét tam giác AEI và tam giác ADI có :
\(\widehat{E}=\widehat{D}\left(=90\right)^o\)
AE = AD ( cmt )
AI chung
=> Tam giác AEI = Tam giác ADI ( ch - cgv)
=> Góc DAI = Góc EAI ( hai góc tương ứng )
Mà AI nằm giữa AB và AC nên AI là đường phân giác của góc BAC( ĐPCM )
+) Gọi điểm H là giao của BC và AI .
Xét tam giác ABC có :
BD là đường cao thứ nhất
CE là đường cao thứ hai
=> AH phải là đường cao thứ ba (t/c đường cao trong tam giác )
=> \(Ah⊥BC\)
Mà I thuộc AH => \(AI⊥BC\)