Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

\(M>\frac{x}{x+y+z+t}+\frac{y}{x+y+z+t}+\frac{z}{x+y+z+t}+\frac{t}{x+y+z+t}=\frac{x+y+z+t}{x+y+z+t}=1\)
Mà \(\frac{a}{b}<1\) thì \(\frac{a}{b}<\frac{a+m}{b+m}\) ; \(m\in N\)*
Do đó \(M<\frac{x+t}{x+y+z+t}+\frac{y+z}{x+y+z+t}+\frac{z+x}{x+y+z+t}+\frac{t+y}{x+y+z+t}=\frac{2\left(x+y+z+t\right)}{x+y+z+t}=2\)
Vậy 1 < M < 2 nên M không phải là số tự nhiên/

Nhận xét z=0 không thỏa mãn giả thiết bài toán.
Đặt z = R , R > 0
Ta có:
2 + i z = z w + 1 - i ⇔ 2 R - 1 + R + 1 i = z w
⇒ R w = 5 R 2 - 2 R + 2 = 5 R 2 - 2 R + 2 R 2 = 5 - 2 R + 2 R 2 = 2 1 R - 1 2 2 + 9 2 ≥ 3 2 , ∀ R > 0
Suy ra w ≤ 2 3 , ∀ R > 0
Ta có
T = w + 1 - i ≤ 1 - i ≤ 2 3 + 2 = 4 2 3
Đẳng thức xảy ra khi z = 2 w = k 1 - i , k > 0 2 + i z = z w + 1 - i
⇔ z = 2 w = 1 3 ( 1 - i )
Vậy m a x T = 4 2 3
Chọn đáp án A.


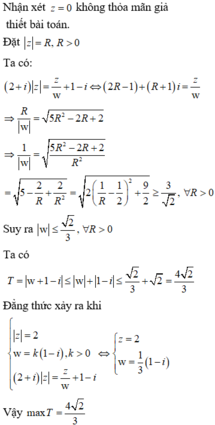
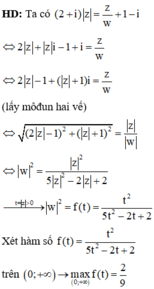




Đáp án là C