Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

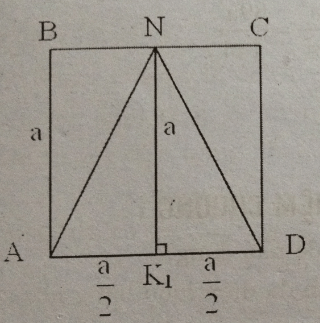
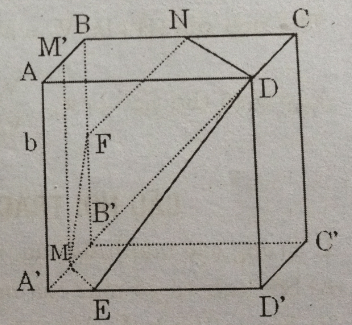
b)-Mặt phẳng (DMN) cắt hình lập phương theo thiết diện MEDNF trong đó ME // ND, FN //DE và chia hình lập phương thành hai khối đa diện (H) và (H’), gọi phần khối lập phương chứa A, B, A’, mặt phẳng (DMN) là (H)
-Chia (H) thành các hình chóp F.DBN, D.ABFMA’ và D.A’EM.

Gọi O là giao điểm của AC và BD \(\Rightarrow A_1O\perp\left(ABCD\right)\)
Gọi E là trung điểm của AD \(\Rightarrow\begin{cases}OE\perp AD\\A_1E\perp AD\end{cases}\)
Suy ra \(\widehat{A_1EO}\) là góc giữa 2 mặt phẳng \(\left(ADD_1A_1\right)\) và \(\left(ABCD\right)\) \(\Rightarrow\widehat{A_1EO}=60^o\)
Suy ra : \(A_1O=OE.\tan\widehat{A_1EO}=\frac{AB}{2}\tan\widehat{A_1EO}=\frac{a\sqrt{3}}{2}\)
Diện tích đáy \(S_{ABCD}=AB.AD=a^2\sqrt{3}\)
Thể tích \(V_{ABCD.A'B'C'D'}=S_{ABCD}.A_1O=\frac{3a^2}{2}\)
Ta có : \(B_1C||A_1D\)\(\Rightarrow B_1C||\left(A_1CD\right)\)
\(\Rightarrow d\left(B_1,\right)\left(A_1BD\right)=d\left(C,\left(A_1BD\right)\right)=CH\)
\(\Rightarrow d\left(B_1,\right)\left(A_1BD\right)=CH=\frac{CD.CB}{\sqrt{CD^2+CB^2}}=\frac{a\sqrt{3}}{2}\)

Gọi H là hình chiếu vuông góc của A' trên mặt phẳng (ABCD)
Kẻ HN vuông góc với AB tại N, HM vuông góc với AD tại M
Ta cần tìm chiều cao h=A'H của hình hộp
Dễ dàng chứng minh \(\widehat{A'NH}=60^0\) và \(\widehat{A'MH}=45^0\)
Xét tam giác vuông NHA' và MHB' có
\(NH=\frac{HA'}{tan\widehat{HNA'}}=\frac{h}{\sqrt{3}}\) và \(MH=\frac{HA'}{tan\widehat{HMA'}}=h\)
Xét hình vuông AMHN có \(AH=\sqrt{HN^2+HM^2}=\frac{2h}{\sqrt{3}}\)
Xét tam giác vuông AHA' có \(AH^2+A'H^2=A'A^2\Leftrightarrow h^2+\frac{4}{3}h^2=1\Leftrightarrow h=\sqrt{\frac{3}{7}}\)
Vậy thể tích hình hộp là: \(V=h.\sqrt{3}.\sqrt{7}=\sqrt{\frac{3}{7}}.\sqrt{3}\sqrt{7}=3\)

Trong mặt phẳng (ABCD), kéo dài AM cắt DC tại E \(\Rightarrow\) C là trung điểm DE (t/c đường trung bình)
Trong mặt phẳng CDD'C' nối EI kéo dài lần lượt cắt CC' và DD' tại P và Q
Mặt phẳng (AMI) cắt lập phương theo thiết diện là tứ giác AMPQ
Gọi N là trung điểm CD \(\Rightarrow\left\{{}\begin{matrix}IN//DD'\\CN=\frac{1}{2}CD\end{matrix}\right.\) \(\Rightarrow\frac{EN}{ED}=\frac{\frac{3a}{2}}{2a}=\frac{3}{4}\)
Talet: \(\frac{EN}{ED}=\frac{IN}{DQ}=\frac{3}{4}\Rightarrow DQ=\frac{4}{3}IN=\frac{4}{3}.\frac{a}{2}=\frac{2a}{3}\)
\(CP=\frac{1}{2}DQ=\frac{a}{3}\) (đường trung bình)
\(V_{MCP.ADQ}=V_{E.ADQ}-V_{E.MCP}=\frac{1}{6}\left(ED.AD.DQ-EC.MC.CP\right)\)
\(=\frac{1}{6}\left(2a.a.\frac{2a}{3}-a.\frac{a}{2}.\frac{a}{3}\right)=\frac{7a^3}{36}\)
\(\Rightarrow V=V_{ABCD.A'B'C'D'}-\frac{7a^3}{26}=a^3-\frac{7a^3}{36}=\frac{29a^3}{36}\)

A B C D S M H
\(\widehat{BAD}=120^0\Rightarrow\widehat{ABC}\Rightarrow\Delta ABC\) đều
\(\Rightarrow AM=\frac{a\sqrt{3}}{2}\Rightarrow S_{ABCD}=\frac{a^3\sqrt{3}}{2}\)
Tam giác SAM vuông tại A có \(\widehat{SMA}=45^0\Rightarrow\) Tam giác SAM vuông tại A : SA = AM = \(\frac{a\sqrt{3}}{2}\)
Do đó \(V_{S.ABCD}=\frac{1}{3}SA.S_{ABCD}=\frac{a^3}{4}\)
Do AD song song với BC nên d(D;(SBC))=d(A,(SBC))
Gọi H là hình chiếu vuông góc của A trên SM
Ta có : \(\begin{cases}AM\perp BC\\SA\perp BC\end{cases}\)\(\Rightarrow BC\perp\cdot\left(SAM\right)\)
\(\Rightarrow BC\perp AH\Rightarrow AH\perp\left(SBC\right)\Rightarrow d\left(A,\left(SBC\right)\right)=AH\)
Ta có :
\(AH=\frac{AM\sqrt{2}}{2}=\frac{a\sqrt{6}}{4}\Rightarrow d\left(D,\left(SBC\right)\right)=\frac{a\sqrt{6}}{4}\)

\(\Delta ABD\) đều cạnh a.
\(\Rightarrow S_{ABD}=\frac{a^2\sqrt{3}}{4}\Rightarrow S_{ABCD}=2S_{ABD}=\frac{a^2\sqrt{3}}{2}\)
\(\Delta ABB'\)vuông tại B \(\Rightarrow BB'=AB\tan30^o=a\sqrt{3}V=B.h=S_{ABCD}.BB'=\frac{3a^3}{2}\)


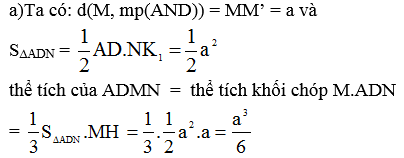
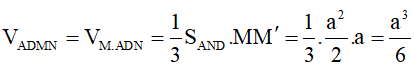

Chọn D
+) Gọi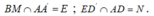
Ta có M là trung điểm của AB
=> M là trung điểm EB'
=> N là trung điểm của ED' và AD
+) Ta có