Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án A
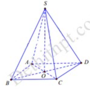
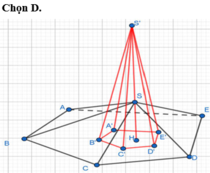
Kí hiệu như hình vẽ với S O ⊥ A B C D và tứ giác ABCD là hình vuông.
Ta có V = 1 3 S O . S A B C D = 1 3 S O . A B 2
Thể tích mới V ' = 1 3 . 1 2 S O . 3 A B 2 = 9 2 V

Đáp án A
Diện tích đáy tăng lên 9 lần và độ dài đường cao xuống hai lần. Khi đó thể tích khối chóp mới là 9 2 V

Đáp án A
Nếu tăng cạnh đáy lên 2 lần thì diện tích đáy sẽ tăng lên 4 lần. Gọi diện tích đáy lúc đầu là S ⇒ diện tích đáy sau khi tăng là 4S.
Gọi chiều cao lúc đầu là h ⇒ chiều cao sau khi giảm là h 4 ⇒ Thể tích lúc đầu bằng thể tích lúc sau = S h 3 ⇒ thể tích không thay đổi.

Đáp án A
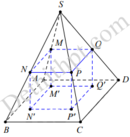
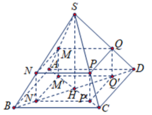
Đặt S M S A = x , vì mặt phẳng M N P Q song song với đáy
Suy ra M N A B = N P B C = P Q C D = M Q A D = x ( định lí Thalet).
Và d M ; A B C D d S ; A B C D = M A S A = 1 − S M S A = 1 − x ⇒ M M ' = 1 − x × h .
Mặt khác d t M N P Q = x 2 × d t A B C D nên thể tích khối đa diện
M N P Q . M ' N ' P ' Q ' là V = M M ' x d t M N P Q
= 1 − x x 2 × h × d t A B C D = 3 x 2 − x 3 × V S . A B C D .
Khảo sát hàm số f x = x 2 − x 3 → m ax 0 ; 1 f x = 4 27 .
Dấu “=” xảy ra ⇔ x = 2 3 .
Vậy S M S A = 2 3 thì thể tích khối hộp M N P Q . M ' N ' P ' Q ' lớn nhất.

Đáp án A
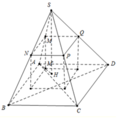
Ta có: S M S A = x = M N A B ⇒ M N = x . A B
Tương tự M Q = x A D
M M ' S H = A M S A = 1 − x ⇒ M M ' = 1 − x S H
Do đó V M N P Q . M ' N ' P ' Q ' = x 2 1 − x . A B . A D . S H .
Xét hàm số f x = x 2 1 − x = x 2 − x 3 ⇒ f ' x = 2 x − 3 x 2
Do đó f ' x = 0 ⇔ x = 2 3 .
Vậy V M N P Q . M ' N ' P ' Q ' = x 2 1 − x . A B . A D . S H lớn nhất khi S M S A = 2 3 .

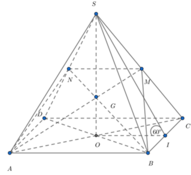




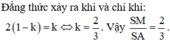
Đáp án A