Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án A
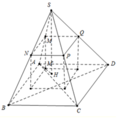
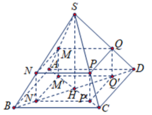
Ta có: S M S A = x = M N A B ⇒ M N = x . A B
Tương tự M Q = x A D
M M ' S H = A M S A = 1 − x ⇒ M M ' = 1 − x S H
Do đó V M N P Q . M ' N ' P ' Q ' = x 2 1 − x . A B . A D . S H .
Xét hàm số f x = x 2 1 − x = x 2 − x 3 ⇒ f ' x = 2 x − 3 x 2
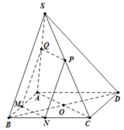
Do đó f ' x = 0 ⇔ x = 2 3 .
Vậy V M N P Q . M ' N ' P ' Q ' = x 2 1 − x . A B . A D . S H lớn nhất khi S M S A = 2 3 .

Đáp án D
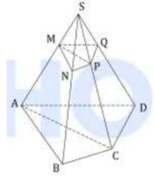
Do α qua M song song với mặt đáy nên em kẻ MN / / AB N ∈ SB ;
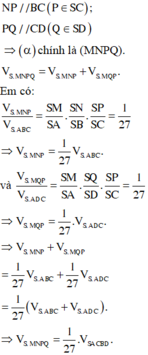
Chú ý: Em nhớ rằng, công thức tính tỉ số thể tích chỉ áp dụng cho khối chóp tam giác. Còn với khối chóp tứ giác, ngũ giác, lục giác,… em cần chia ra thành các khối chóp tam giác và áp dụng công thức.
Công thức giải nhanh:
Cắt khối chóp bởi mặt phẳng song song với đáy: Xét khối chóp S . A 1 A 2 . .. A n , mặt phẳng (P) song song với mặt đáy cắt cạnh SA 1 tại m thỏa mãn SM SA 1 = k . Khi đó (P) chia khối chóp thành 2 khối đa diện, trong đó khối đa diện chứa đỉnh S có thể tích V' và khối đa diện ban đầu có thể tích V thì V ' V = k 3
Nên ⇒ V SMNPQ V SABCD = ( 1 3 ) 2 = 1 27

Đáp án B
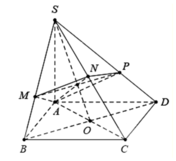
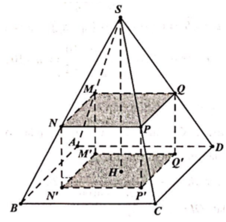
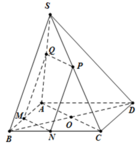
Nối S O ∩ A N = E , qua E kẻ đường thẳng song song với BD. Cắt SB,SD lần lượt tại M , P ⇒ m p P ≡ A M N P .
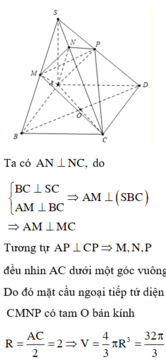
Ta có S A ⊥ A B , S A ⊥ A D ⇒ S A ⊥ A B C D ⇒ B C ⊥ S A B .
Mà SC ⊥ A M N P ⇒ S C ⊥ A M suy ra A M ⊥ S B C .
Do đó A M ⊥ M C mà O là trung điểm của A C ⇒ O A = O M = O C .
Tương tự, ta chứng minh được O là tâm mặt cầu ngoại tiếp khối
đa diện A B C D . M N P ⇒ R = A C 2 = 4 a 3 2 = 2 a 3 .
Vậy thể tích cần tính là V = 4 3 π R 3 = 4 3 π 2 3 3 = 32 3 π a 3 .


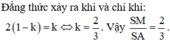


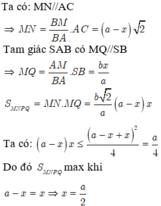
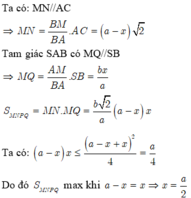
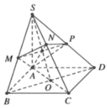

Đáp án A
Đặt S M S A = x , vì mặt phẳng M N P Q song song với đáy
Suy ra M N A B = N P B C = P Q C D = M Q A D = x ( định lí Thalet).
Và d M ; A B C D d S ; A B C D = M A S A = 1 − S M S A = 1 − x ⇒ M M ' = 1 − x × h .
Mặt khác d t M N P Q = x 2 × d t A B C D nên thể tích khối đa diện
M N P Q . M ' N ' P ' Q ' là V = M M ' x d t M N P Q
= 1 − x x 2 × h × d t A B C D = 3 x 2 − x 3 × V S . A B C D .
Khảo sát hàm số f x = x 2 − x 3 → m ax 0 ; 1 f x = 4 27 .
Dấu “=” xảy ra ⇔ x = 2 3 .
Vậy S M S A = 2 3 thì thể tích khối hộp M N P Q . M ' N ' P ' Q ' lớn nhất.