Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án D
Giả sử (P) cắt cạnh AA’ tại M sao cho A'M = x
Chọn hệ trục tọa độ như hình vẽ
B ( 0 ; 0 ; 1 ) , D ' ( 1 ; 1 ; 0 ) , M ( 1 ; 0 ; x ) ⇒ B D ' → ( 1 ; 1 ; − 1 ) , B M → ( 0 ; − 1 ; x + 1 ) ⇒ [ B D ' → , B M → ] = ( x ; − x − 1 ; − 1 )
Thiết diện BMD’N thu được là hình bình hành nên
S B M D ' N = 2 S B M D ' = [ B D ' → , B M → ] = x 2 + ( x + 1 ) 2 + 1 y = 2 x 2 + 2 x + 2 ⇒ y ' = 4 x + 2 y ' = 0 ⇔ x = − 1 2 ⇒ S min = 6 2

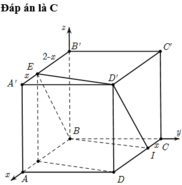
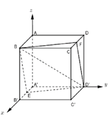
Mặt phẳng (P) cắt hình lập phương theo thiết diện là hình bình hành BID’E.
Hình chiếu vuông góc của bình hành BID’E xuống mặt phẳng (ABCD) là hình bình hành BIDF.
Gọi φ là góc tạo bởi (P) và mặt phẳng (ABCD).
Ta có: cos φ = S B I D F S B I D ' E .
Đặt hình lập phương vào hệ tọa độ như hình vẽ. B ≡ O; Ox ≡ BA; Oy ≡ BC; Oz ≡ BB’
Đặt A’E = x.
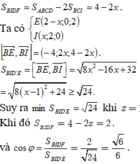

Nguyễn Thị Thu Hà thật là oai oai oai học giỏi mà bài tổng và hiệu cũng hỏi người khác

Đáp án D
Phương pháp: Gắn hệ trục tọa độ Oxyz để giải bài toán.
Cách giải: Giả sử mặt phẳng chứa AC’ cắt hình lập phương theo thiết diện là tứ giác AEC’F ![]()
Ta có: 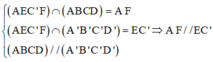
Tương tự ta chứng minh được AE//FC’
=>AEC’ F là hình bình hành ![]()
Gắn hệ trục tọa độ như hình vẽ sao cho A’(0;0;0); B’(2;0;0); C’(2;2;0); D’(0;2;0); A(0;0;2); B(2;0;2); C(2;2;2); D(0;2;2)
Gọi E(x;0;0) (0≤x≤2) ta có:
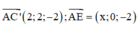
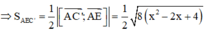
Ta có ![]()
Dấu bằng xảy ra ó x = 1, khi đó ![]()

vì (C) đi qua điểm A nên tọa độ điểm A thỏa mãn pt \(y=\frac{ax^2-bx}{x-1}\) ta có \(\frac{5}{2}=\frac{a+b}{-2}\Rightarrow a+b=-5\)
vì tiếp tuyến của đồ thị tại điểm O có hệ số góc =-3 suy ra y'(O)=-3
ta có \(y'=\frac{ax^2-2ax+b}{\left(x-1\right)^2}\) ta có y'(O)=b=-3 suy ra a=-2
vậy ta tìm đc a và b

hoành độ giao điểm là nghiệm của pt
\(x^3-3mx^2+3\left(2m-1\right)x+1=2mx-4m+3\Leftrightarrow x^3-3mx^2+4mx-3x-2+4m=0\Leftrightarrow x^3-3x-2-m\left(3x^2-4x+4\right)=0\)
giải hệ pt ta có \(C_m\) luôn đi qua điểm A là nghiệm của hệ pt sau
\(\begin{cases}3x^2-4x+4=0\\x^3-3x-2=0\end{cases}\)
ta đc điều phải cm

hoành độ giao điểm là nghiệm của pt
\(x^3+3x^2+mx+1=1\Leftrightarrow x\left(x^2+3x+m\right)=0\)
\(x=0;x^2+3x+m=0\)(*)
để (C) cắt y=1 tại 3 điểm phân biệt thì pt (*) có 2 nghiệm phân biệt khác 0
\(\Delta=3^2-4m>0\) và \(0+m.0+m\ne0\Leftrightarrow m\ne0\)
từ pt (*) ta suy ra đc hoành độ của D, E là nghiệm của (*)
ta tính \(y'=3x^2+6x+m\)
vì tiếp tuyến tại Dvà E vuông góc
suy ra \(y'\left(x_D\right).y'\left(x_E\right)=-1\)
giải pt đối chiếu với đk suy ra đc đk của m

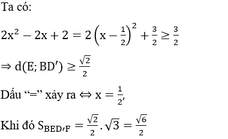
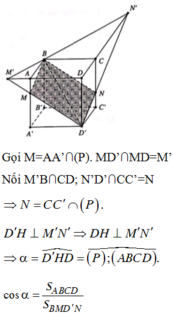

Đáp án D
Giả sử (P) cắt cạnh AA’ tại M sao cho A'M = x
Chọn hệ trục tọa độ như hình vẽ
B(0;0;1), D'(1;1;0), M(1;0;x)
B D ' → 1 ; 1 ; - 1 , B M → 0 ; - 1 ; x + 1 ⇒ B D ' → , B M → = x ; - x - 1 ; - 1
Thiết diện BMD’N thu được là hình bình hành nên