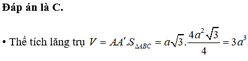
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

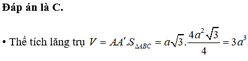

Áp dụng BĐT tam giác ta có:
a+b>c =>c-a<b =>c2-2ac+a2<b2
a+c>b =>b-c <a =>b2-2bc+c2<a2
b+c>a =>a-b<c =>a2-2ab+b2<c2
Suy ra: c2-2ac+a2+b2-2bc+c2+a2-2ab+b2<a2+b2+c2
<=>-2.(ab+bc+ca)+2.(a2+b2+c2)<a2+b2+c2
<=>-2(ab+bc+ca)<-(a2+b2+c2)
<=>2.(ab+bc+ca)<a2+b2+c2

a) (n + 2) chia hết cho (n - 1). \(\left(n\in N\right)\)
\(\Rightarrow\) n - 2 + 4 chia hết cho n - 1
\(\Rightarrow\) 4 chia hết cho n - 1
\(\Rightarrow\) n - 1 \(\in\) Ư(4) = {1; 2; 4;}
\(\Rightarrow\) n \(\in\) {2; 3; 5}
b) (2n + 7) chia hết cho (n + 1). \(\left(n\in N\right)\)
\(\Rightarrow\) 2n + 2 + 5 chia hết cho n + 1
\(\Rightarrow\) 2(n + 1) + 5 chia hết cho n + 1
\(\Rightarrow\) 5 chia hết cho n + 1
\(\Rightarrow\) n + 1 \(\in\) Ư(5) = {1; 5;}
\(\Rightarrow\) n \(\in\) {0; 4}
c) (2n + 1) chia hết cho (6 - n). \(\left(n\in N\right)\)
\(\Rightarrow\) (12 - 2n) - (12 - n) + (2n + 1) chia hết cho 6 - n
\(\Rightarrow\) 2(6 - n) - 12 + n + 2n + 1 chia hết cho 6 - n
\(\Rightarrow\) -12 + 3n + 1 chia hết cho 6 - n
\(\Rightarrow\) 18 - 3n - 12 + 1 chia hết cho 6 - n
\(\Rightarrow\) 3(6 - n) - 12 + 1 chia hết cho 6 - n
\(\Rightarrow\) -11 chia hết cho 6 - n
\(\Rightarrow\) 6 - n \(\in\) Ư(-11) = {-1; 1; -11; 11}
\(\Rightarrow\) Không có số tự nhiên n thỏa mãn
d) 3n chia hết cho (5 - 2n) \(\left(n\in N\right)\)
\(\Rightarrow\) 3n chia hết cho 5 - n - n
\(\Rightarrow\) 15 - 4n - 4n chia hết cho 5 - n - n
\(\Rightarrow\) 3(5 - n - n) chia hết cho 5 - n - n
KL: Theo đề bài, ta có \(\left(n\in N\right)\) sao cho 3n chia hết cho (5 - 2n) và 2n < 5
\(\Rightarrow\) n \(\in\) {0; 1; 2}
e) (4n + 3) chia hết cho (2n + 6) \(\left(n\in N\right)\)
\(\Rightarrow\) (2n + 6) + (2n + 6) - 9 chia hết cho 2n + 6
\(\Rightarrow\) 2(2n + 6) - 9 chia hết cho 2n + 6
\(\Rightarrow\) - 9 chia hết cho 2n + 6
\(\Rightarrow\) 2n + 6 \(\in\) Ư(-9) = {-1; 1; -3; 3; -9; 9}
\(\Rightarrow\) Không có số tự nhiên n thỏa mãn
a) (n + 2) chia hết cho (n - 1). \(\left(n\in N\right)\)
\(\Rightarrow\) n - 2 + 4 chia hết cho n - 1
\(\Rightarrow\) 4 chia hết cho n - 1
\(\Rightarrow\) n - 1 \(\in\) Ư(4) = {1; 2; 4;}
\(\Rightarrow\) n \(\in\) {2; 3; 5}
b) (2n + 7) chia hết cho (n + 1). \(\left(n\in N\right)\)
\(\Rightarrow\) 2n + 2 + 5 chia hết cho n + 1
\(\Rightarrow\) 2(n + 1) + 5 chia hết cho n + 1
\(\Rightarrow\) 5 chia hết cho n + 1
\(\Rightarrow\) n + 1 \(\in\) Ư(5) = {1; 5;}
\(\Rightarrow\) n \(\in\) {0; 4}
c) (2n + 1) chia hết cho (6 - n). \(\left(n\in N\right)\)
\(\Rightarrow\) (12 - 2n) - (12 - n) + (2n + 1) chia hết cho 6 - n
\(\Rightarrow\) 2(6 - n) - 12 + n + 2n + 1 chia hết cho 6 - n
\(\Rightarrow\) -12 + 3n + 1 chia hết cho 6 - n
\(\Rightarrow\) 18 - 3n - 12 + 1 chia hết cho 6 - n
\(\Rightarrow\) 3(6 - n) - 12 + 1 chia hết cho 6 - n
\(\Rightarrow\) -11 chia hết cho 6 - n
\(\Rightarrow\) 6 - n \(\in\) Ư(-11) = {-1; 1; -11; 11}
\(\Rightarrow\) Không có số tự nhiên n thỏa mãn
d) 3n chia hết cho (5 - 2n) \(\left(n\in N\right)\)
\(\Rightarrow\) 3n chia hết cho 5 - n - n
\(\Rightarrow\) 15 - 4n - 4n chia hết cho 5 - n - n
\(\Rightarrow\) 3(5 - n - n) chia hết cho 5 - n - n
KL: Theo đề bài, ta có \(\left(n\in N\right)\) sao cho 3n chia hết cho (5 - 2n) và 2n < 5
\(\Rightarrow\) n \(\in\) {0; 1; 2}
e) (4n + 3) chia hết cho (2n + 6) \(\left(n\in N\right)\)
\(\Rightarrow\) (2n + 6) + (2n + 6) - 9 chia hết cho 2n + 6
\(\Rightarrow\) 2(2n + 6) - 9 chia hết cho 2n + 6
\(\Rightarrow\) - 9 chia hết cho 2n + 6
\(\Rightarrow\) 2n + 6 \(\in\) Ư(-9) = {-1; 1; -3; 3; -9; 9}
\(\Rightarrow\) Không có số tự nhiên n thỏa mãn

2.
Gọi quãng đường cần tìm là s.---> vận tốc Xuân= s/12,
--> vận tốc Hạ=s/10
thời gian Xuân gặp Hạ: 50/(s/12)= (s-50)/(s/10)
50x12/s= (s-50)x10/s
50x12=10s-500
---> s = (500+50x12)/10= 110
quãng đường giữa nhà hai bạn là 110m
4.
Khi ngược dòng 1 giờ ta đi được số phần quãng sông là:
1 : 8 = 1/8 (quãng sông)
Khi xuôi dòng 1 giờ ta đi được số phần quãng sông là:
1 : 4 = 1/4 (quãng sông)
Bèo trôi theo ta về 1 giờ trôi được số phần quãng sông là:
(1/4 - 1/8) : 2 = 1/16 (quãng sông)
Bèo trôi theo ta về cập bến sau số giờ là:
1 : 1/16 = 16 (giờ)
Đ/s: 16 giờ

* Sửa:
a) 35 - (-x + 8) = 23 - (-7)
35 + x - 8 = 30
35 + x = 30 + 8
35 + x = 38
x = 38 - 35
x = 3
Vậy, x = 3
b) 4 - 2(x - 3) = 3 (3 - x)
4 - (2x - 2 . 3) = 3 . 3 - 3x
4 - (2x - 6) = 9 - (2x + x)
4 - 2x + 6 = 9 - 2x - x
(4 + 6) = 9 - x
10 = 9 - x
9 - 10 = x
-1 = x
x = -1
Vậy, x = -1

a) Vì x.y= -21 suy ra x;y thuộc Ư(21)={ -1,-3,-7,-21,1,3,7,21 }
( rồi em tự suy ra các cặp x,y nhé )

a d e m n b c i h
a, tam giác ade cân a
=> góc d = góc e và ad = ae
tam giác adb = tam giác aec ( cgc)
=> ab=ac
=> tam giác abc cân a
b, tam giác bmd vuông m và tam giác cne vuông n
góc m = góc n =90 độ
góc d = góc e
bd = ce
=> bmd = cne (ch-gn)
=> bm = cn
c, có tam giác bmd = tam giác cne
=> góc mbd = góc nce
mà góc cbi đối đỉnh góc mbd, bci đối đỉnh nce
=> góc cbi = góc bci
=> tam giác ibc cân i
d, lây h là trung điểm bc
tam giác abc cân a có ah là đường trung tuyến úng với bc
=> ah vừa là trung tuyến vừa là đường cao ứng với bc
cmtt với ibc => ih vừa là trung tuyến vừa là đường cao ứng với bc
=> a,i,h thẳng hàng
=> ai vừa trung tuyến vừa là đường cao tam giác abc cân a
=> đpcm

ta tính \(y'=6x^2+a-12\)
để hàm số vừa có cực đại và cực tiểu thì \(y'=0\) hai nghiệm phân biệt suy ra \(6x^2+a-12=0\Leftrightarrow6x^2=12-a\) (*)
để (*) có 2 nghiệm phân biệt thì \(12-a>0\Leftrightarrow a<12\)
vậy với a<12 thì hàm số có cực đại và cực tiểu
gọi \(x_1;x_2\) là cực đại và cực tiểu của hàm số
suy ra \(x_{1,2}=\pm\sqrt{\frac{12-a}{6}}\) ta thay vào hàm số suy ra đc \(y_{1,2}\) suy ra \(I\left(x_1;y_1\right);A\left(x_2;y_2\right)\)
sử dụng công thức tính khoảng cách
pt đường thẳng y có dạng x=0
ta có \(d\left(I;y\right)=\frac{\left|x_1\right|}{\sqrt{1}}\); \(d\left(A;y\right)=\frac{\left|x_2\right|}{\sqrt{1}}\)
\(d\left(I,y\right)=d\left(A,y\right)\) giải pt ta tìm ra đc a

Chọn B.
Phương pháp:
Áp dụng công thức tính thể tích lăng trụ: V = B.h trong đó: V là thể tích lăng trụ, B là diện tích đáy của lăng trụ, h là chiều cao của lăng trụ.
Cách giải:
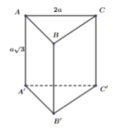
Diện tích tam giác đều ABC có cạnh 2a là: