Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án B
Xét lăng trụ (T) có:
![]()
Xét mặt cầu (C) có: R C = A P 2 = a 3
![]()
Tỉ số bằng 8 4 3 = 2 3 3

Chọn A.
Để ý rằng hai khối lăng trụ đó có diện tích đáy bằng nhau, tỉ số hai đường cao tương ứng bằng 1/2.
a.1/2
okkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkk

Câu 5:
Tương tự câu 4, ta thấy tâm $I$ của khối cầu ngoại tiếp $S.ABCD$ là trung điểm $SC$
Theo định lý Pitago:
$SA^2=SB^2-AB^2=(a\sqrt{3})^2-a^2=2a^2$
$AC^2=AB^2+BC^2=a^2+a^2=2a^2$
$SC=\sqrt{SA^2+AC^2}=\sqrt{2a^2+2a^2}=2a$
Do đó: $R=SI=IC=\frac{SC}{2}=a$
Thể tích khối cầu ngoại tiếp S.ABCD là:
$V=\frac{4}{3}\pi R^3=\frac{4}{3}\pi a^3$
Đáp án A
Câu 4:
$AC=\sqrt{AB^2+AD^2}=2a$
$(SC, (ABCD))=\widehat{SCA}=60^0$
$\Rightarrow \frac{SA}{AC}=\tan \widehat{SCA}=\tan 60^0=\sqrt{3}$
$\Rightarrow SA=\sqrt{3}.AC=2\sqrt{3}a$
$SC=\sqrt{SA^2+AC^2}=\sqrt{(2\sqrt{3}a)^2+(2a)^2}=4a$
Gọi $I$ tâm mặt cầu ngoại tiếp hình chóp. $IS=IA=IC$ nên $I$ là tâm ngoại tiếp tam giác $SAC$
$\Rightarrow I$ là trung điểm $SC$.
Bán kính $IS=IC=\frac{AC}{2}=\frac{4a}{2}=2a$
Đáp án A

O A B C D B' A' D' C' M K O a a
a. Từ giả thiết ta có :
\(C\left(a;a;0\right);C'\left(a;a;b\right);D'\left(0;a;b\right);B'\left(a;0;b\right)\)
Vì M là trung điểm của CC' nên \(M=\left(a;a;\frac{b}{2}\right)\)
Ta có :
\(\overrightarrow{BD}=\left(-a;a;0\right)\)
\(\overrightarrow{BA}=\left(-a;0;b\right)\)
\(\overrightarrow{BM}=\left(0;a;\frac{b}{2}\right)\)
Vì thế \(\left[\overrightarrow{BD};\overrightarrow{BA'}\right]=\left(\left|\begin{matrix}a&0\\0&b\end{matrix}\right|;\left|\begin{matrix}0&-a\\b&-a\end{matrix}\right|;\left|\begin{matrix}-a&a\\-a&0\end{matrix}\right|\right)\)
\(=\left(ab,ab,a^2\right)\)
Vậy \(V_{BDa'M}=\frac{1}{6}\left|\left[\overrightarrow{BD};\overrightarrow{BA'}\right].\overrightarrow{BM}\right|=\frac{1}{6}\left|a^2b+\frac{a^2b}{2}\right|=\frac{a^2b}{4}\)
b. Gọi K là trung điểm của BD. Do \(A'B=A'D\Rightarrow A'K\perp BD\)
Lại có \(MB=MD\Rightarrow MK\perp BD\)
Vậy \(\widehat{A'KM}=90^0\)
\(\Leftrightarrow\overrightarrow{A'K}.\overrightarrow{MK}=0\)
Ta có :
\(K=\left(\frac{a}{2};\frac{a}{2};0\right)\) do đó :
\(\overrightarrow{A'K}=\left(\frac{a}{2};\frac{a}{2};-b\right)\)
\(\overrightarrow{MK}=\left(-\frac{a}{2};\frac{-a}{2};\frac{-b}{2}\right)\)
Vậy \(\left(1\right)\Leftrightarrow-\frac{a^2}{4}-\frac{a^2}{4}+\frac{b^2}{2}=0\)
\(\Leftrightarrow b^2=a^2\)
\(\Leftrightarrow\frac{a}{b}=1\)
Do (a>0,b>0) vì thế \(\left(A'BD\right)\perp\left(MBD\right)\Leftrightarrow\frac{a}{b}=1\)
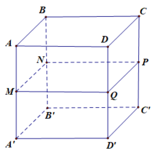



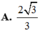
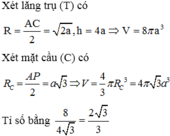
Đáp án A
A B C D . A ' B ' C ' D ' nội tiếp khối lăng trụ, ABCD.MNPQ nội tiếp mặt cầu nên
A B C D . A ' B ' C ' D ' là hình hộp chữ nhật
Bán kính đường tròn ngoại tiếp
ABCD là r = 2 a , V T = 4 a . π . 2 a 2 = 8 πa 3
Bán kính mặt cầu ngoại tiếp ABCD.MNPQ là
Vậy V ( T ) V ( C ) = 8 πa 3 4 3 πa 3 = 2 3 3