Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
a: góc ABC=1/2*sđ cung AC=90 độ
góc ABD=1/2*180=90 độ
góc CBD=góc ABC+góc ABD=90+90=180 độ
=>C,B,D thẳng hàng
b: góc AFC=1/2*sđ cung AC=90 độ
=>CF vuông góc AD
góc AED=1/2*180=90 độ
=>DE vuông góc AC
góc CED=góc CFD=90 độ
=>CEFD nội tiếp
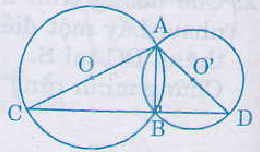
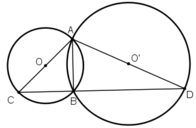
Nối B với 3 điểm A, C, D ta có:
=
(góc nội tiếp chắn nửa đường tròn)
=
( góc nội tiếp chắn nửa đường tròn)
Vậy +
=
Suy ra ba điểm A, C, D thẳng hàng.
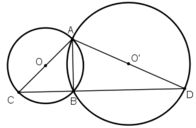
Trong đường tròn tâm O,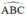 
là góc nội tiếp chắn nửa đường tròn
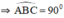
Trong đường tròn tâm O’, 
là góc nội tiếp chắn nửa đường tròn
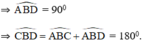
Suy ra, ba điểm C, B và D thẳng hàng.
Trong đường tròn tâm O,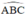 
là góc nội tiếp chắn nửa đường tròn
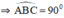
Trong đường tròn tâm O’, 
là góc nội tiếp chắn nửa đường tròn
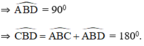
Suy ra, ba điểm C, B và D thẳng hàng.
Kiến thức áp dụng
+ Trong một đường tròn, góc nội tiếp chắn nửa đường tròn là góc vuông.
Vì góc ACB là có nội tiếp chắn nửa đường tròn của (O)
=> góc ACB= 90 độ
Xét (I) có góc MCN là góc nội tiếp chắn cung MN
mà góc MCN= 90 độ
=> MN là đường kính của (I)
=> 3 điểm M,I,N thẳng hàng
b) vì Δ CIN cân tại I( IC=IN=R)
=> góc ICN= góc INC
lại có Δ COB cân tại O(OC=OB=R)
=> góc OCB= góc OBC
=> góc INC= góc OBC ( cùng = góc OCB)
mà 2 góc này ở vị trí đồng vị của 2 đường thẳng MN và AB
=> MN // AB
lại có ID vuông góc với AB
=> ID vuông góc với MN( đpcm)
A B C O D E H I F
a) Xét \(\Delta ABE\)và \(\Delta ABD\)có :
\(\widehat{BAE}=\widehat{BAD}\); \(\widehat{ABE}=\widehat{BDE}\)
\(\Rightarrow\Delta ABE\approx\Delta ADB\left(g.g\right)\)
\(\Rightarrow\frac{AB}{AE}=\frac{AD}{AB}\Rightarrow AD.AE=AB^2\)( 1 )
Xét \(\Delta ABO\)vuông tại B ( do AB là tiếp tuyến ), đường cao BH ( tự c/m ), ta có hệ thức lượng
\(AH.AO=AB^2\)( 2 )
Từ ( 1 ) và ( 2 ) suy ra \(AD.AE=AH.AO=AB^2\)
b) \(AD.AE=AH.AO\Rightarrow\frac{AE}{AH}=\frac{AO}{AD}\)
Xét \(\Delta AEH\)và \(\Delta AOD\)có :
\(\frac{AE}{AH}=\frac{AO}{AD}\); \(\widehat{EAH}\)( chung )
\(\Rightarrow\Delta AEH\approx\Delta AOD\left(c.g.c\right)\)\(\Rightarrow\widehat{AHE}=\widehat{ADO}\)( 3 )
Mà \(\Delta ODE\)cân tại O ( do OE = OD ) \(\Rightarrow\widehat{OED}=\widehat{ODE}\)( 4 )
Từ ( 3 ) và ( 4 ) suy ra \(\widehat{AHE}=\widehat{OED}\)
c) đường thẳng qua B vuông góc với CD tại I
Xét hai tam giác vuông BID và CBI có :
\(\widehat{IDB}=\widehat{CBI}\); \(\widehat{BID}=\widehat{BIC}=90^o\)
\(\Rightarrow\Delta BID\approx\Delta CIB\left(g.g\right)\) \(\Rightarrow\frac{ID}{IB}=\frac{IB}{IC}=\frac{DB}{BC}\)
\(\Rightarrow\frac{ID}{IB}.\frac{IB}{IC}=\frac{ID}{IC}=\frac{BD^2}{BC^2}\)
Mặt khác : \(\Delta DAC\)có : BI // AC
\(\Rightarrow\frac{FI}{AC}=\frac{DI}{DC}=\frac{DI}{DI+CI}=\frac{1}{1+\frac{CI}{DI}}=\frac{1}{1+\frac{BC^2}{BD^2}}=\frac{BD^2}{BD^2+BC^2}=\frac{BD^2}{4R^2}\)( R là bán kính )
\(\Rightarrow FI=\frac{BD^2.AC}{4R^2}\)( 5 )
Xét \(\Delta BCD\)và \(\Delta ACO\)có :
\(\widehat{BCD}=\widehat{OAC}\); \(\widehat{CBD}=\widehat{ACO}=90^o\)
\(\Rightarrow\Delta BCD\approx\Delta CAO\left(g.g\right)\)\(\Rightarrow\frac{BC}{AC}=\frac{BD}{OC}\Rightarrow BC=\frac{AC.BD}{R}\)( 6 )
Xét 2 tam giác vuông BIC và BCD có :
\(\widehat{BCD}\)( chung ) ; \(\widehat{BIC}=\widehat{CBD}=90^o\)
\(\Rightarrow\Delta BIC\approx\Delta DBC\)( g.g )
\(\Rightarrow\frac{IB}{BD}=\frac{BC}{CD}\Rightarrow IB=\frac{BC.BD}{2R}\)( 7 )
Từ ( 6 ) và ( 7 ) suy ra : \(IB=\frac{AC.BD^2}{2R^2}\)( 8 )
Từ ( 5 ) và ( 8 ) suy ra : \(IF=\frac{IB}{2}\Rightarrow\)F là trung điểm của IB
\(\Rightarrow HF\)là đường trung bình của \(\Delta BCI\)\(\Rightarrow HF//CD\)
Tam giác ABC nội tiếp trong đường tròn (O) có AC là đường kính nên góc (ABC) = 90 °
Tam giác ABD nội tiếp trong đường tròn (O’) có AD là đường kính nên góc (ABD) = 90 °
Ta có: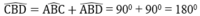
Vậy ba điểm C, B, D thẳng hàng và AB ⊥ CD