
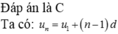
![]()
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

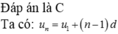
![]()

ta có U6+U8=2U1+12d=-18
\(U^2_3+U^2_5=2U^2_1+12Ud+12d^2=-26\)
từ đó bằng phương pháp giải hệ 2 pt trên là ra
Đoạn \(2u_1^2+2ud+12d^2\) em ko hiểu lắm chị ơi :o Em đã giải bài toán này theo cách bên dưới nhưng ra nghiệm rất xấu (ko biết có đúng không?). Em ko hiểu mình đã gặp vấn đề chỗ nào? Mong được kiểm tra giúp ạ? thanks



a) Ta có:
{5u1+10u=0S4=14{5u1+10u=0S4=14
⇔{5u1+10(u1+4d)=04(2u1+3d)2=14⇔{3u1+8d=02u1+3d=7⇔{u1=8d=−3⇔{5u1+10(u1+4d)=04(2u1+3d)2=14⇔{3u1+8d=02u1+3d=7⇔{u1=8d=−3
Vậy số hạng đầu u1 = 8, công sai d = -3
b) Ta có:
{u7+u15=60u24+u212=1170⇔{(u1+6d)+(u1+14d)=60(1)(u1+3d)2+(u1+11d)2=1170(2){u7+u15=60u42+u122=1170⇔{(u1+6d)+(u1+14d)=60(1)(u1+3d)2+(u1+11d)2=1170(2)
(1) ⇔ 2u1 + 20d = 60 ⇔ u1 = 30 – 10d thế vào (2)
(2) ⇔[(30 – 10D) + 3d]2 + [(30 – 10d) + 11d]2 = 1170
⇔ (30 – 7d)2 + (30 + d)2 = 1170
⇔900 – 420d + 49d2 + 900 + 60d + d2 = 1170
⇔ 50d2 – 360d + 630 = 0
⇔[d=3⇒u1=0d=215⇒u1=−12⇔[d=3⇒u1=0d=215⇒u1=−12
Vậy
{u1=0d=3{u1=0d=3
hay
{u1=−12d=215

S= u1.u1 + u2.u2+...+un.un
S = u1.(u2 - d) + u2.(u3 - d)+...+un(un+1 - d)
S = u1.u2 + u2.u3 +...+un.un+1-d(u1+u2+...+un)
Đặt A = u2.u3 + u3.u4+...+un.un+1
3d.A = u2.u3.(u4-u1) + u3.u4.(u5-u2)+...+un.un+1.(un+2-un-1)
3d.A = u2.u3.u4 - u1.u2.u3 + u3.u4.u5 - u2.u3.u4+...+un.un+1.un+2 - un-1.un.un+1
3d.A = un.un+1.un+2 - u1.u2.u3
3d.A = (u1 + d.n - d)(u1 + d.n)(u1 + d.n + d) - u1.(u1+d).(u1+2.d)
A = [(u1 + d.n - d)(u1 + d.n)(u1 + d.n + d) - u1.(u1+d).(u1+2.d)]/(3.d)
S = A + u1.(u1 + d) + d[2.u1+(n-1).d].n/2

\(\lim\limits_{x\rightarrow1}\frac{x^{2016}+x-2}{\sqrt{2018x+1}-\sqrt{x+2018}}=\lim\limits_{x\rightarrow1}\frac{2016x^{2015}+1}{\frac{1009}{\sqrt{2018x+1}}-\frac{1}{2\sqrt{x+2018}}}=\frac{2017}{\frac{1009}{\sqrt{2019}}-\frac{1}{2\sqrt{2019}}}=2\sqrt{2019}\)
Để hàm liên tục tại \(x=1\)
\(\Rightarrow\lim\limits_{x\rightarrow1}f\left(x\right)=f\left(1\right)\Rightarrow k=2\sqrt{2019}\)
2.
\(\lim\limits_{x\rightarrow1}\frac{x^2+ax+b}{x^2-1}=\frac{1}{2}\Leftrightarrow\left\{{}\begin{matrix}a+b+1=0\\\lim\limits_{x\rightarrow1}\frac{2x+a}{2x}=\frac{1}{2}\end{matrix}\right.\)
\(\Rightarrow\left\{{}\begin{matrix}a+b=-1\\\frac{a+2}{2}=\frac{1}{2}\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}a=-1\\b=0\end{matrix}\right.\) \(\Rightarrow S=1\)
3.
\(\lim\limits_{x\rightarrow1}\frac{\sqrt{x^2+x+2}-2+2-\sqrt[3]{7x+1}}{\sqrt{2}\left(x-1\right)}=\lim\limits_{x\rightarrow1}\frac{\frac{\left(x-1\right)\left(x+2\right)}{\sqrt{x^2+x+2}+2}-\frac{7\left(x-1\right)}{\sqrt[3]{\left(7x+1\right)^2}+2\sqrt[3]{7x+1}+4}}{\sqrt{2}\left(x-1\right)}\)
\(=\lim\limits_{x\rightarrow1}\frac{1}{\sqrt{2}}\left(\frac{x+2}{\sqrt{x^2+x+2}+2}-\frac{7}{\sqrt[3]{\left(7x+1\right)^2}+2\sqrt[3]{7x+1}+4}\right)\)
\(=\frac{1}{\sqrt{2}}\left(\frac{3}{4}-\frac{7}{12}\right)=\frac{\sqrt{2}}{12}\)
\(\Rightarrow a+b+c=1+12+0=13\)