Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

cho 2014=2013+1 thay vào ta có:\(B=x^{2013}-\left(2013+1\right)x^{2012}+\left(2013+1\right)x^{2011}-...-\left(2013+1\right)x^2+\left(2013+1\right)x-1\)
\(=x^{2013}-\left(x+1\right)x^{2012}+\left(x+1\right)x^{2011}-...-\left(x+1\right)x^2+\left(x+1\right)x-1\)
\(=x^{2013}-x^{2013}-x^{2012}+x^{2012}+x^{2011}-...-x^3-x^2+x^2+x-1\)
\(=x-1=2013-1=2012\)

\(Q=\frac{a}{b+c}+\frac{b}{a+c}+\frac{c}{a+b}\)
\(=>Q=\left(\frac{a}{b+c}+1\right)+\left(\frac{b}{a+c}+1\right)+\left(\frac{c}{a+b}+1\right)-3\)
\(=>Q=\left(\frac{a+b+c}{b+c}\right)+\left(\frac{a+b+c}{a+c}\right)+\left(\frac{a+b+c}{a+b}\right)-3\)
\(=>Q=\left(a+b+c\right).\left(\frac{1}{b+c}+\frac{1}{a+c}+\frac{1}{a+b}\right)-3\)
\(=>Q=259.15-3=3882\)
Vậy Q=3882
\(Q=\frac{a}{b+c}+\frac{b}{a+c}+\frac{c}{a+b}=\frac{259-\left(b+c\right)}{b+c}+\frac{259-\left(a+c\right)}{a+c}+\frac{259-\left(a+b\right)}{a+b}\)
\(=259.\left(\frac{1}{a+b}+\frac{1}{b+c}+\frac{1}{a+c}\right)+\left[\frac{-\left(b+c\right)}{b+c}+\frac{-\left(a+c\right)}{a+c}+\frac{-\left(a+b\right)}{a+b}\right]\)
tới đây tự làm tiếp

15.
Ta có \(a+b+c+ab+bc+ac=6\)
Mà \(ab+bc+ac\le\left(a+b+c\right)^2\)
=> \(\left(a+b+c\right)^2+\left(a+b+c\right)-6\ge0\)
=> \(a+b+c\ge3\)
\(A=\frac{a^4}{ab}+\frac{b^4}{bc}+\frac{c^4}{ac}\ge\frac{\left(a^2+b^2+c^2\right)^2}{ab+bc+ac}\ge a^2+b^2+c^2\ge\frac{1}{3}\left(a+b+c\right)^2\ge3\)(ĐPCM)
Bài 18, Đặt \(\left(a^2-bc;b^2-ca;c^2-ab\right)\rightarrow\left(x;y;z\right)\) thì bđt trở thành
\(x^3+y^3+z^3\ge3xyz\)
\(\Leftrightarrow x^3+y^3+z^3-3xyz\ge0\)
\(\Leftrightarrow\left(x+y+z\right)\left(x^2+y^2+z^2-xy-yz-zx\right)\ge0\)
\(\Leftrightarrow\frac{1}{2}\left(x+y+z\right)\left[\left(x-y\right)^2+\left(y-z\right)^2+\left(z-x\right)^2\right]\ge0\)
Vì \(\left(x-y\right)^2+\left(y-z\right)^2+\left(z-x\right)^2\ge0\)nên ta đi chứng minh \(x+y+z\ge0\)
Thật vậy \(x+y+z=a^2-bc+b^2-ca+c^2-ab\)
\(=\frac{1}{2}\left[\left(a-b\right)^2+\left(b-c\right)^2+\left(c-a\right)^2\right]\ge0\)(đúng)
Tóm lại bđt được chứng minh
Dấu "=": tại a=b=c

11/Theo BĐT AM-GM,ta có; \(ab.\frac{1}{\left(a+c\right)+\left(b+c\right)}\le\frac{ab}{4}\left(\frac{1}{a+c}+\frac{1}{b+c}\right)\)\(=\frac{1}{4}\left(\frac{ab}{a+c}+\frac{ab}{b+c}\right)\)
Tương tự với hai BĐT kia,cộng theo vế và rút gọn ta được đpcm.
Dấu "=" xảy ra khi a= b=c
Ơ vãi,em đánh thiếu abc dưới mẫu,cô xóa giùm em bài kia ạ!
9/ \(VT=\frac{\Sigma\left(a+2\right)\left(b+2\right)}{\left(a+2\right)\left(b+2\right)\left(c+2\right)}\)
\(=\frac{ab+bc+ca+4\left(a+b+c\right)+12}{\left(ab+bc+ca\right)+4\left(a+b+c\right)+8+abc+\left(ab+bc+ca\right)}\)
\(\le\frac{ab+bc+ca+4\left(a+b+c\right)+12}{\left(ab+bc+ca\right)+4\left(a+b+c\right)+9+3\sqrt[3]{\left(abc\right)^2}}\)
\(=\frac{ab+bc+ca+4\left(a+b+c\right)+12}{ab+bc+ca+4\left(a+b+c\right)+12}=1\left(Q.E.D\right)\)
"=" <=> a = b = c = 1.
Mong là lần này không đánh thiếu (nãy tại cái tội đánh ẩu)
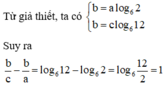


Chọn đáp án B.
DISCOVERY
Một cách tổng quát chúng ta có các kết quả sau:
1) Cho các số thực dương m, n, p khác 1 và thỏa mãn m.p = n α
Nếu tồn tại các số thực a, b, c thỏa mãn hệ thức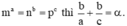
2) Cho các số thực dương m, n, p khác 1 và thỏa mãn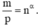
Nếu tồn tại các số thực a, b, c thỏa mãn hệ thức