Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

+ Ta có hàm số g(x) = x 3 - 3 x 2 + 2 = m là hàm số chẵn nên đồ thị nhận trục Oy làm trục đối xứng.
+ Khi x≥ 0 ; g(x) = x3- 3x2+ 2
Do đó; đồ thị hàm số g(x) = x 3 - 3 x 2 + 2 có dạng như hình vẽ.
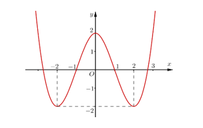
+ Dựa vào đồ thị suy ra phương trình x 3 - 3 x 2 + 2 = m có nhiều nghiệm thực nhất khi và chỉ khi -2< m< 2.
Chọn C.

Đặt \(\sqrt{-x^2+2x+15}=t\Rightarrow0\le t\le4\)
BPT trở thành:
\(-4t\ge-t^2+2+m\)
\(\Leftrightarrow t^2-4t-2\ge m\)
\(\Rightarrow m\le\min\limits_{\left[0;4\right]}\left(t^2-4t-2\right)\)
Xét \(f\left(t\right)=t^2-4t-2\) trên \(\left[0;4\right]\)
\(-\dfrac{b}{2a}=2\in\left[0;4\right]\)
\(f\left(0\right)=f\left(4\right)=-2\) ; \(f\left(2\right)=-6\)
\(\Rightarrow f\left(t\right)_{min}=-6\Rightarrow m\le-6\)

+ Xét hàm số f( x) = x3- x2+ ( m2+ 1) x- 4m- 7 trên đoạn [ 0; 2]
Ta có f’ (x) = 3x2- 2x+ m2+ 1= 3( x-1/3) 2+ m2+ 2/3> 0 .
+ Suy ra hàm số f(x) đồng biến trên
0 ; 2 ⇒ m i n [ 0 ; 2 ] f ( x ) = f ( 0 ) = - 4 m - 7 m a x [ 0 ; 2 ] f ( x ) = f ( 2 ) = 2 m 2 - 4 m - 1
+ Khi đó
m a x [ 0 ; 2 ] y = m a x [ 0 ; 2 ] f ( x ) = m a x - 4 m - 7 ; 2 m 2 - 4 m - 1 ≤ 15 ⇔ - 4 m - 7 ≤ 15 2 m 2 - 4 m - 1 ≤ 15 ⇔ - 11 2 ≤ m ≤ 2 2 m 2 - 4 m - 16 ≤ 0 ⇔ - 11 2 ≤ m ≤ 2 - 2 ≤ m ≤ 4 ⇔ - 2 ≤ m ≤ 2 → m ∈ ℤ m ∈ ± 2 ; ± 1 ; 0
Vậy có 5 giá trị thoả mãn.
Chọn C.

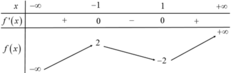

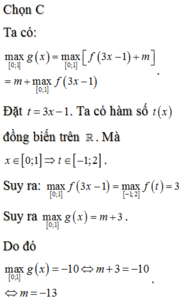
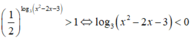
Chọn D