Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Gia tốc tự do trên mặt đất (h<<R)
\(g_1=\frac{GM}{R^2}\Rightarrow GM=g_1.R^2\)
Gia tốc tự do ở độ cao \(h=\frac{R}{4}\) :
\(g_2=\frac{GM}{\left(R+h\right)^2}=\frac{g_1.R^2}{\left(R+\frac{R}{4}\right)^2}\)
\(\Leftrightarrow g_2=\frac{9,8.R^2}{\frac{25}{16}R^2}=6,272\left(m/s^2\right)\)

Ta có
g=\(\dfrac{G.M}{r^2}\)=9,8
=>G.M=9,8.r2
gh=\(\dfrac{G.M}{(r+h)^2}\)=\(\dfrac{9,8.r^2}{(r+r/2)^2}\)=9,8r2:(3/2 .r)2=9,8r2:(9/4.r2)=4,3(5)m/s2
g1=\(\dfrac{G.M}{\left[r+h\right]^2}\)=\(\dfrac{G.M}{\left[2h+h\right]^2}\)=\(\dfrac{G.M}{\left[r+\dfrac{1}{2}r\right]^2}\)=\(\dfrac{G.M}{\left[\dfrac{3}{2}r\right]^2}\)
g2=\(\dfrac{G.M}{r^2}\)
=>\(\dfrac{g_1}{g_2}\)=\(\dfrac{r^2}{\dfrac{9}{4}r^2}\) <=>\(\dfrac{9,8}{g_2}\)=\(\dfrac{9}{4}\)
<=>g2=9,8/\(\dfrac{9}{4}\) \(\simeq\)4,36 m/s2

1.
gọi m là trọng lượng vật, M là trọng lượng trái đất
trọng lực của vật bằng lực hấp dẫn trái đất tác dụng lên vật
tại mặt đất \(F_{hd0}=P_0\Leftrightarrow P_0=\dfrac{G.m.M}{R^2}\)
tại vị trí h \(F_{hd}=P\Leftrightarrow P=\dfrac{G.m.M}{\left(R+h\right)^2}\)
lấy P chia P0
\(\Leftrightarrow\dfrac{P}{P_0}=\dfrac{R^2}{\left(R+h\right)^2}\) với h=R
\(\Leftrightarrow\dfrac{P}{600}=\dfrac{1}{4}\Rightarrow P=150N\) (R+h=2R)
2.
gọi m là trọng lượng vật, M là trọng lượng trái đất
\(g_0=\dfrac{G.M}{R^2}\) (1)
gia tốc của vật ở độ cao h1=10000m
\(g=\dfrac{G.M}{\left(R+h_1\right)^2}\) (2)
lấy (2) chia (1)\(\Rightarrow\dfrac{g}{g_0}=\dfrac{R^2}{\left(R+h_1\right)^2}\Rightarrow g\approx9,77\)m/s2
ở độ cao h=\(\dfrac{R}{2}\)
\(g_1=\dfrac{G.M}{\left(R+h\right)^2}\) (3)
lấy (3) chia (1)\(\Rightarrow\dfrac{g_1}{g_0}=\dfrac{R^2}{\left(R+h\right)^2}\Rightarrow\)\(\dfrac{g_1}{g_0}=\dfrac{1}{\left(\dfrac{9}{4}\right)}\)\(\Rightarrow g_1=\)4,36m/s2
3.
như bài 2 nên mình làm tắt
\(\dfrac{g}{g_0}=\dfrac{R^2}{\left(R+h\right)^2}\)\(\dfrac{4,9}{9,8}\)
\(\Rightarrow\dfrac{R}{R+h}=\dfrac{\sqrt{2}}{2}\Rightarrow h=\).........
4.
\(\dfrac{P}{P_0}=\dfrac{R^2}{\left(R+h\right)^2}=\dfrac{50}{450}\Rightarrow\dfrac{R}{R+h}=\dfrac{1}{3}\Rightarrow h=2R\)
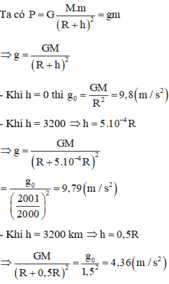
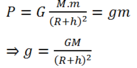
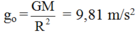
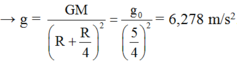
Đáp án B