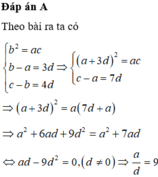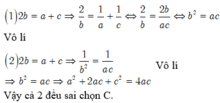Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án D
Phương pháp:
Sử dụng công thức tổng quát của CSC ![]() và tính chất của CSN
và tính chất của CSN ![]()
Cách giải:
a, b, c lần lượt là số thứ nhất, thứ tư và thứ tám của một cấp số cộng công sai là s ≠ 0
nên ta có 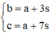 a, b, c theo thứ tự tạo thành một cấp số nhân với công bội khác 1 nên ta có
a, b, c theo thứ tự tạo thành một cấp số nhân với công bội khác 1 nên ta có
![]()
![]()
![]()

Chọn C
Gọi ba số đó lần lượt là x,y,z
Do ba số là các số hạng thứ 2, thứ 9 và thứ 44 của một cấp số cộng nên ta có liên hệ: y = x + 7 d , z = x + 42 (với d là công sai của cấp số cộng)
Theo giả thiết ta có: x + y + z = x + x + 7 d + x + 42 d = 3 x + 49 d = 217
Mặt khác do x,y,z là các số hạng liên tiếp của một cấp số nhân nên
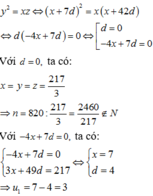
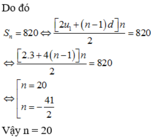

vì (C) đi qua điểm A nên tọa độ điểm A thỏa mãn pt \(y=\frac{ax^2-bx}{x-1}\) ta có \(\frac{5}{2}=\frac{a+b}{-2}\Rightarrow a+b=-5\)
vì tiếp tuyến của đồ thị tại điểm O có hệ số góc =-3 suy ra y'(O)=-3
ta có \(y'=\frac{ax^2-2ax+b}{\left(x-1\right)^2}\) ta có y'(O)=b=-3 suy ra a=-2
vậy ta tìm đc a và b

9/10 số thứ nhất.
80,01 – 19,233 = 60,777
Số thứ nhất:
60,777 : 9 x 10 = 67,53
Số thứ hai:
80,01 – 67,53 = 12,48
Hiệu hai số đó là:
67,53 – 12,48 = 55,05