Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

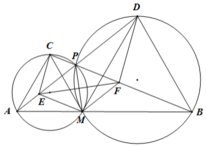
c) Ta có EF là đường trung trực của PM ⇒ EP = EM ⇒ ∆ EPM cân tại E
Mặt khác EPM = ACM = 60o (do AMPC là tứ giác nội tiếp) nên ∆ EPM đều
⇒ PE = PM . Tương tự PF = PM
Ta có CM // DB nên PCM = PBD
Mà BMPD là tứ giác nội tiếp nên PBD = PMD. Suy ra PCM = PMD
Ta lại có CPM = DPM = 120o ⇒ Δ C P M ~ Δ M P D ( g . g ) ⇒ C P M P = P M P D ⇒ C P P F = P E P D
Theo định lý Talét đảo ta có CE // DF ⇒ CDFE là hình thang.

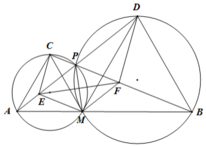
b) Vì AMPC là tứ giác nội tiếp nên
C P M = 180 o − C A M = 120 o = C M B ⇒ Δ C P M ~ Δ C M B ( g . g ) ⇒ C P C M = C M C B ⇒ C P . C B = C M 2 ⇒ C P . C B = C M .
Tương tự D P . D A = D M
Vậy C P . C B + D P . D A = C M + D M = A M + B M = A B

Không vẽ hình vì sợ duyệt nhé.
Tứ giác ADNM nội tiếp nên \(\widehat{ADM}=\widehat{ANM}\)
Tứ giác AMCD là hình vuông nên \(\widehat{ADM}=45^0\)
Từ đó \(\widehat{ANM}=45^0\)
Tứ giác BENM nội tiếp nên \(\widehat{ENM}+\widehat{EBN}=180^0\)\(\Rightarrow\widehat{ENM}=180^0-\widehat{EBM}\)
Tứ giác BMEF là hình vuông nên \(\widehat{EBM}=45^0\)
Từ đó \(\widehat{ENM}=180^0-45^0=135^0\)
Ta có \(\widehat{ANE}=\widehat{ANM}+\widehat{ENM}=45^0+135^0=180^0\)
Từ đó ta có A, N, E thẳng hàng.

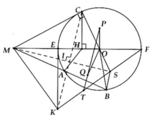
a, HS tự chứng minh
b, MH.MO = MA.MB ( = M C 2 )
=> ∆MAH:∆MOB (c.g.c)
=> M H A ^ = M B O ^
M B O ^ + A H O ^ = M H A ^ + A H O ^ = 180 0
=> AHOB nội tiếp
c, M K 2 = ME.MF = M C 2 Þ MK = MC
∆MKS = ∆MCS (ch-cgv) => SK = SC
=> MS là đường trung trực của KC
=> MS ^ KC tại trung của CK
d, Gọi MS ∩ KC = I
MI.MS = ME.MF = M C 2 => EISF nội tiếp đường tròn tâm P Þ PI = PS. (1)
MI.MS = MA.MB (= M C 2 ) => AISB nội tiếp đường tròn tâm Q Þ QI = QS. (2)
Mà IT = TS = TK (do DIKS vuông tại I). (3)
Từ (1), (2) và (3) => P, T, Q thuộc đường trung trực của IS => P, T, Q thẳng hàng
a) Vì C M A = D M B = 60 o ⇒ C M B = D M A = 120 o . Xét ∆ CMB và ∆ AMD có
C M = A M C M B = D M A ⇒ Δ C M B = Δ A M D ( c . g . c ) M B = M D ⇒ M C B = M A D M B C = M D A
Suy ra AMPC và BMPD là các tứ giác nội tiếp