Cho a < b, hãy so sánh:a) a + 1 và b + 1; b) 2 - a và 2

Khách

Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Mua vip

Pham Trong Bach

11 tháng 3 2019

Cho a < b, hãy so sánh:

a) a + 1 và b + 1; b) 2 - a và 2 - b

#Toán lớp 8

Cao Minh Tâm

11 tháng 3 2019

Đúng(0)

Các câu hỏi dưới đây có thể giống với câu hỏi trên

Trần Đỗ Nhật Linh

11 tháng 5 2019 - olm

a, Tìm các số tự nhiên x thỏa mãn bất phương trình sau: 5x - 2 \(\le\) 2x -8

b, Cho \(\frac{1}{5}a-4< \frac{1}{5}b-4\)Hãy so sánh a và b

c, Chứng minh (a+b)²\(\ge\) 4ab

Giúp mình với!! Mình đang cần gấp

#Toán lớp 8

Quỳnh Thơ

16 tháng 1 2019 - olm

1. Cho a < b so sánh 2a và 2b + 1; -3a và -3b - 1

2. Cho a > b > 0 CMR \(\frac{1}{a}< \frac{1}{\text{b}}\)

3. CMR

a. \(\left(x+y\right)^2< 2.\left(x^2+y^2\right)\)

b. \(x^2+y^2+z^2+3\ge2.\left(x+y+z\right)\)

Mọi người giải hộ mình với ạ

Giải được câu nào cũng được :> thanks trước ạ

#Toán lớp 8

Pham Van Hung

16 tháng 1 2019

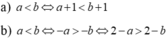
1. \(a< b\Leftrightarrow2a< 2b\Leftrightarrow2a+1< 2b+1\)

\(a< b\Leftrightarrow-3a>-3b\Leftrightarrow-3a>-3b-1\)

2.\(a>b>0\Leftrightarrow a.\frac{1}{ab}>b.\frac{1}{ab}\Leftrightarrow\frac{1}{b}>\frac{1}{a}\Leftrightarrow\frac{1}{a}< \frac{1}{b}\)

Đúng(0)

huongkarry

10 tháng 8 2017 - olm

Cho A=\(\frac{1981-1980}{1981+1980}\)và B=\(\frac{1981^2-1980^2}{1981^2+1980^2}\). Hãy so sánh A và B

#Toán lớp 8

Le Nhat Phuong

10 tháng 8 2017

Do phần B đc tính theo lũy thừa nên

\(A< B\)

Vậy....

Đúng(0)

Đặng Khánh Linh

19 tháng 3 2017 - olm

Cho a>b>0 . So sánh : a=\(\frac{1+a}{1+a+a^2}\) và b=\(\frac{1+b}{1+b+b^2}\)

#Toán lớp 8

Mai Chu Sơn

25 tháng 3 2019 - olm

Cho a,b,c > 0. CMR \(\frac{a}{b}< \frac{a+c}{b+c}\). Áp dụng so sánh \(A=\frac{10^{17}+1}{10^{16}+1}\)Và \(B=\frac{10^{16}+1}{10^{15}+1}\)

#Toán lớp 8

zZz Cool Kid_new zZz

25 tháng 3 2019

sai đề rồi bạn.\(\frac{a}{b}>\frac{a+c}{b+c}\) với \(a>b\) mới đúng nha.

Ta có:\(A=\frac{10^{17}+1}{10^{16}+1}>\frac{10^{17}+1+9}{10^{16}+1+9}=\frac{10^{17}+10}{10^{16}+10}=\frac{10\left(10^{16}+1\right)}{10\left(10^{15}+1\right)}=\frac{10^{16}+1}{10^{15}+1}\)

\(\Rightarrow A>B\)

Đúng(0)

Nguyễn Minh Nga

25 tháng 3 2019

:DDDDDD

Đúng(0)

Sách Giáo Khoa

5 tháng 5 2017

Cho \(a>0,b>0\), nếu \(a< b\) hãy chứng tỏ :

a) \(a^2< ab\) và \(ab< b^2\)

b) \(a^2< b^2\) và \(a^3< b^3\)

#Toán lớp 8

Ha Hoang Vu Nhat

5 tháng 5 2017

a. Do \(a>0,\) \(b>0\) \(\Rightarrow a,b\) là số dương

Ta có:

* \(a< b\Leftrightarrow a^2< ab\) (nhân cả hai vế với a)

* \(a< b\Leftrightarrow ab< b^2\) (nhân cả hai vế với b)

b. Từ câu a theo tính chất bắc cầu suy ra:\(a^2< b^2\)

Ta có: \(a^2< b^2\Leftrightarrow a^3< ab^2\) (nhân cả hai vế với a)

mà ab²<b³ (a<b)

\(\Rightarrow a^3< b^3\)

Đúng(0)

Luzo Anh

23 tháng 7 2016 - olm

So sánh A và B:

a/ A=\(\left(2+1\right)\left(2^2+1\right)\left(2^4+1\right)\left(2^8+1\right)\left(2^{16}+1\right)\)

B=\(2^{32}\)

b/ A= \(2015.2017\) và B=\(2016^2\)

#Toán lớp 8

Hoàng Lê Bảo Ngọc

23 tháng 7 2016

a) \(A=\left(2-1\right)\left(2+1\right)\left(2^2+1\right)\left(2^4+1\right)\left(2^8+1\right)\left(2^{16}+1\right)\)

\(=\left(2^2-1\right)\left(2^2+1\right)\left(2^4+1\right)\left(2^8+1\right)\left(2^{16}+1\right)\)

\(=.............................................................\)

\(=\left(2^{16}-1\right)\left(2^{16}+1\right)=2^{32}-1=B-1\)

Suy ra A < B

b) \(A=2015.2017=\left(2016-1\right)\left(2016+1\right)=2016^2-1=B-1\)

Suy ra A < B

Đúng(0)

Mai Phương Uyên

23 tháng 7 2016

Phần a bạn nhân thêm ở A là (2-1) là ra hằng đẳng thức, cứ thế mà triển. (Kết quả: A<B)

Phần b: phân tích A, ta có:

2015.2017= (2016-1).(2016+1)= 2016^2 -1 <2016^2

Suy ra: A<B

Đúng(0)

Sách Giáo Khoa

22 tháng 4 2017

Cho \(a< b\), hãy so sánh :

2a và 2b; 2a và a + b; -a và -b

#Toán lớp 8

Tuyết Nhi Melody

22 tháng 4 2017

Ta có:

a < b và 2 > 0 => 2a < 2b

a < b cộng hai vế với a

=> a + a < a + b => 2a < a + b

a < b và -1 < 0 => -a > -b

Đúng(0)

tuan anh luong

15 tháng 4 2018

https://i.imgur.com/j3XSqUo.jpg

Đúng(0)

Nguyễn Quang Hùng

10 tháng 7 2018 - olm

1.tìm x, biết:

a)√x < 3

b)x²= 5

c)√x <√2

2.So sánh

a)√3 - 5 và -2

b)2-√2 và 1 phần 2

Giúp mình với

#Toán lớp 8

Kiên-Messi-8A-Boy2k6

10 tháng 7 2018

Vì \(\sqrt{x}\ge0\Rightarrow0\le\sqrt{x}< 3\)

\(\Rightarrow0\le x< 9\Rightarrow x\in\left\{0;1;2;...;8\right\}\)

\(b,x^2=5\)

\(\Rightarrow\sqrt{x^2}=\pm\sqrt{5}\)

\(\Rightarrow x=\pm\sqrt{5}\)

c, Ta có:\(x\ne0\left(\sqrt{x}\ge0\forall x\right)\)

\(\Rightarrow\sqrt{0}\le\sqrt{x}< \sqrt{2}\)

\(\Rightarrow0\le x< 4\)

\(\Rightarrow x\in\left\{0;1;2;3\right\}\)

Đúng(0)

Mạnh Nguyễn Đức

23 tháng 7 2016 - olm

cho a,b,c tm a+b+c >0 và -1 < a,b,c < 1

cm \(^{a^2}\)+\(^{b^2}\)+\(^{c^2}\) <2

#Toán lớp 8

Mạnh Nguyễn Đức

23 tháng 7 2016

ai giúp tôi vs

Đúng(0)

Chúng tôi đề xuất

Tài nguyên

Ứng dụng mobile

Bảng xếp hạng

Các khóa học có thể bạn quan tâm

Yêu cầu VIP