Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) 1cm + 2cm = 3cm < 4cm
⇒ bộ ba đoạn thẳng 1cm, 2cm, 4cm không thể tạo thành 1 tam giác.
b) 2cm + 3cm = 5cm.
⇒ Bộ ba đoạn thẳng 2cm; 3cm; 5cm không lập thành tam giác.
c) Ta có 3cm + 4cm = 7cm > 5cm.
Do đó bộ đoạn thẳng 3cm, 4cm, 5cm có thể thành 3 cạnh của tam giác.
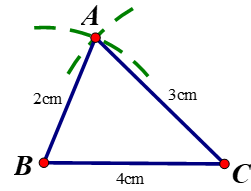
Cách dựng tam giác có ba độ dài 3cm, 4cm, 5cm :
- Vẽ BC = 4cm
- Dựng đường tròn tâm B bán kính 2cm ; đường tròn tâm C bán kính 3cm. Hai đường tròn cắt nhau tại A. Nối AB, AC ta được tam giác cần dựng.

Hình tự vẽ
phần a cậu có thể tự làm :))
b+c)Xét \(\Delta\)ABD và\(\Delta\) EBD có:
AB=AE(gt)
BD(chung)
góc B1 = góc B2
=> \(\Delta\)ABD=\(\Delta\)EBD
=> AD=DE
=>\(\Delta\)ADE cân tại D(2)
Mà BD là tia pg(1)
Từ (1) và (2) => BD là đường cao của tam giác ABC
=> BD\(\perp\) AE
~Hok tốt~
\(\Delta\)
À ừ :vv tớ giải all lại nek
a) \(\Delta\)ABC là tam giác vuông
b+c) Xét \(\Delta\)ABD và \(\Delta\) EBD có:
AB=BE(gt)
BD(chung)
Góc B1=góc B2
=>\(\Delta\)ABD=\(\Delta\)EBD
=>AD= ED
=>\(\Delta\)ADE cân tại D(1)
Mà BD là tí pg của góc B(2)
Từ (1) và (2) => BD là đường cao của \(\Delta\)ABC
=>BD\(\perp\)AE
d) Ta có: BD\(\perp\) FC
AE\(\perp\)BC
Mà D là trực tâm
=> AE // FC
~Hok tốt :^~

Ta có
a)BC^2=10^2=100
AB^2+BC^2=6^2+8^2=36+64=100
Vậy tam giác ABC là tam giác vuông
b)MQ^2=202
MN^2+NQ^2=9^2+11^2=201
Vậy tam giacs MNQ là tam giác vuông
c)CA^2=5^2=25
AB^2+CB^2=3^2+4^2=9+16=25
Vây tam giác ABC là tam giác vuông
d)ABC không phải tam giác vuông
e)NQ^2=9^2=81
MN^2+MQ^=6^2+4^=36+16=52
Vậy tam giác MNQ không phải tam giác vuông

Câu 6 : cho tam giác ABC có AB = 5cm ; BC = 8 cm ; AC = 10 cm . so sánh nào sau đây là dúng
A. B < C < A
B. C < A < B
C. A < B <C
D. C < B < A
Câu 7 : cho Δ ABC cán tại A có A = 50 thì số đo của B là
A. 50 B.100 C. 65 D.130
Câu 8 : bộ 3 đoạn thẳng có độ dài nào sau đây có thể là đọ dài 3 cạnh của một Δ vuông :
A. 3cm; 9cm; 14cm
B. 2cm; 3cm; 5cm
C. 4cm; 9cm; 12cm
D. 6cm; 8cm; 10cm
Câu 9: A

Câu 2:
Ta có: \(\hept{\begin{cases}f\left(0\right)=1\\f\left(1\right)=2\\f\left(2\right)=4\end{cases}}\Rightarrow\hept{\begin{cases}a.0^2+b.0+c=1\\a.1^2+b.1+c=2\\a.2^2+b.2+c=4\end{cases}}\)
\(\Rightarrow\hept{\begin{cases}c=1\\a+b+c=2\\4a+2b+c=4\end{cases}}\Leftrightarrow\hept{\begin{cases}a+b=1\\4a+2b=3\end{cases}}\)
\(\Leftrightarrow\hept{\begin{cases}2a+2b=2\\4a+2b=3\end{cases}}\Rightarrow\left(4a+2b\right)-\left(2a+2b\right)=3-2\)
\(\Leftrightarrow2a=1\Rightarrow a=\frac{1}{2}\)
\(\Rightarrow b=\frac{1}{2}\)
Vậy \(\left(a;b;c\right)=\left(\frac{1}{2};\frac{1}{2};1\right)\)
3) Đáp án đúng: D
Vì \(6^2+8^2=36+64=100=10^2\)
(Định lý Pythagoras đảo)
=> Bộ số 6cm, 8cm, 10cm có thể là độ dài 3 cạnh của tam giác vuông

Ap dụng định lý Pytago vào tam giác vuông ABC ta có:
\(AB^2+AC^2=BC^2\)
\(\Leftrightarrow\)\(BC^2=3^2+4^2=25\)
\(\Leftrightarrow\)\(BC=\sqrt{25}=5\)
Vậy \(BC=5cm\)
Ta có tam giác ABC vuông tại A. Áp dụng định lí Py - ta - go ta có:
BC2 = AB2 + AC2 = 32 + 42 = 25 \(\Rightarrow\)BC = \(\sqrt{25}=5\)
Vậy chọn đáp án B
`A. 3 cm, 3cm, 4cm`
Theo bất đẳng thức trong tam giác, ta có:
`3+3>4`
`->`\(\text{ Bộ ba độ dài này là độ dài 3 cạnh của 1 tam giác (k t/m)}\)
`B. 6cm, 10cm, 8 cm`
Theo bất đẳng thức trong tam giác, ta có:
`6+8>10`
`->`\(\text{ Bộ ba độ dài này là độ dài 3 cạnh của 1 tam giác (k t/m)}\)
`C.3cm, 4cm, 5cm`
Theo bất đẳng thức trong tam giác, ta có:
`3+4>5`
`->`\(\text{ Bộ ba độ dài này là độ dài 3 cạnh của 1 tam giác (k t/m)}\)
`D. 4cm, 8cm, 12cm`
Theo bất đẳng thức trong tam giác, ta có:
`4+8=12`
`->`\(\text{ Bộ ba độ dài này không phải là độ dài 3 cạnh của 1 tam giác (t/m)}\)
Xét các đáp án trên `-> D.`
Chọn D