
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

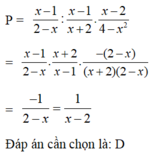

Rút gọn : \(P=\left(\frac{1}{x-2}-\frac{1}{x+2}+1\right):\frac{1}{x^2-4}\)
\(P=\left(\frac{x+2}{x^2-4}-\frac{x-2}{x^2-4}+\frac{\left(x+2\right)\left(x-2\right)}{x^2-4}\right):\frac{1}{x^2-4}\)
\(P=\frac{x+2-x+2+x^2-4}{x^2-4}:\frac{1}{x^2-4}\)
\(P=\frac{x^2}{x^2-4}.\frac{x^2-4}{1}\)
\(P=x^2\)
........
mk chỉ biết làm rút gọn thôi nha

Bài 1:
a: \(A=\dfrac{x+1+x}{x+1}:\dfrac{3x^2+x^2-1}{x^2-1}\)
\(=\dfrac{2x+1}{x+1}\cdot\dfrac{\left(x+1\right)\left(x-1\right)}{\left(2x+1\right)\left(2x-1\right)}=\dfrac{x-1}{2x-1}\)
b: Thay x=1/3 vào A, ta được:
\(A=\left(\dfrac{1}{3}-1\right):\left(\dfrac{2}{3}-1\right)=\dfrac{-2}{3}:\dfrac{-1}{3}=2\)

a) Ta có: A = \(\left(\frac{x}{x-1}+\frac{x}{x^2-1}\right):\left(\frac{2}{x^2}-\frac{2-x^2}{x^3+x^2}\right)\)
A = \(\left(\frac{x\left(x+1\right)}{\left(x-1\right)\left(x+1\right)}+\frac{x}{\left(x-1\right)\left(x+1\right)}\right):\left(\frac{2\left(x+1\right)}{x^2\left(x+1\right)}-\frac{2-x^2}{x^2\left(x+1\right)}\right)\)
A = \(\left(\frac{x^2+x+x}{\left(x-1\right)\left(x+1\right)}\right):\left(\frac{2x+2-2+x^2}{x^2\left(x+1\right)}\right)\)
A = \(\left(\frac{x^2+2x}{\left(x-1\right)\left(x+1\right)}\right):\left(\frac{x^2+2x}{x^2\left(x+1\right)}\right)\)
A = \(\frac{x\left(x+2\right)}{\left(x-1\right)\left(x+1\right)}\cdot\frac{x^2\left(x+1\right)}{x\left(x+2\right)}\)
A = \(\frac{x^2}{x+1}\)
b) ĐKXĐ: x \(\ne\)\(\pm\)1; x \(\ne\)0; x \(\ne\)-2
Ta có: A = 4
<=> \(\frac{x^2}{x+1}=4\)
<=> x2 = 4(x + 1)
<=> x2 - 4x - 4 = 0
<=>(x2 - 4x + 4) - 8 = 0
<=> (x - 2)2 = 8
<=> \(\orbr{\begin{cases}x-2=\sqrt{8}\\x-2=-\sqrt{8}\end{cases}}\)
<=> \(\orbr{\begin{cases}x=2\sqrt{2}+2\\x=2-2\sqrt{2}\end{cases}}\)(tm)
Vậy ...
c) Ta có: A < 0
<=> \(\frac{x^2}{x+1}< 0\)
Do x2 \(\ge\)0 => x + 1 < 0
=> x < -1
Vậy để A < 0 thì x < -1 và x khác -2

Dài quá trôi hết đề khỏi màn hình: nhìn thấy câu nào giải cấu ấy
Bài 4:
\(A=\frac{\left(x-1\right)+\left(x+1\right)}{\left(x+1\right)\left(x-1\right)}-\frac{2}{\left(x+1\right)\left(x-1\right)}=\frac{2\left(x-1\right)}{\left(x-1\right)\left(x+1\right)}\)
a) DK x khác +-1
b) \(dk\left(a\right)\Rightarrow A=\frac{2}{\left(x+1\right)}\)
c) x+1 phải thuộc Ước của 2=> x=(-3,-2,0))
1. a) Biểu thức a có nghĩa \(\Leftrightarrow\hept{\begin{cases}x+2\ne0\\x^2-4\ne0\end{cases}}\)
\(\Leftrightarrow\hept{\begin{cases}x+2\ne0\\x-2\ne0\\x+2\ne0\end{cases}}\)
\(\Leftrightarrow\hept{\begin{cases}x\ne-2\\x\ne2\end{cases}}\)
Vậy vs \(x\ne2,x\ne-2\) thì bt a có nghĩa
b) \(A=\frac{x}{x+2}+\frac{4-2x}{\left(x-2\right)\left(x+2\right)}\)
\(=\frac{x\left(x-2\right)}{\left(x+2\right)\left(x-2\right)}+\frac{4-2x}{\left(x+2\right)\left(x-2\right)}\)
\(=\frac{x^2-2x+4-2x}{\left(x+2\right)\left(x-2\right)}\)
\(=\frac{x^2-4x+4}{\left(x+2\right)\left(x-2\right)}\)
\(=\frac{\left(x-2\right)^2}{\left(x+2\right)\left(x-2\right)}\)
\(=\frac{x-2}{x+2}\)
c) \(A=0\Leftrightarrow\frac{x-2}{x+2}=0\)
\(\Leftrightarrow x-2=\left(x+2\right).0\)
\(\Leftrightarrow x-2=0\)
\(\Leftrightarrow x=2\)(ko thỏa mãn điều kiện )
=> ko có gía trị nào của x để A=0

a, \(M=\sqrt{x^2-4x+4}-\sqrt{x^2+4x+4}\) (ĐK : \(\forall x\in R\))
\(=\sqrt{\left(x-2\right)^2}-\sqrt{\left(x+2\right)^2}\)
* Nếu x\(\ge2\Rightarrow M=x-2-x-2=-4\)
*Nếu x<2 => M=2-x-x-2=-2x
b,Để M=2\(\ne-4\)
=>M=-2x
=>-2x=-4
=>x=2
__________________________________________________________________________________________
P=\(\sqrt{x+2\sqrt{x-1}}+\sqrt{x-2\sqrt{x-1}}\)
\(=\sqrt{x-1+2\sqrt{x-1}+1}+\sqrt{x-1-2\sqrt{x-1}+1}\)
\(=\sqrt{\left(\sqrt{x-1}+1\right)^2}+\sqrt{\left(\sqrt{x-1}-1\right)^2}\)
* Nếu \(x\ge2\Rightarrow P=\sqrt{x-1}+1+\sqrt{x-1}-1=2\sqrt{x-1}\)
* Nếu x<2 =>P=\(\sqrt{x-1}+1+1-\sqrt{x-1}=2\)
VẬY.......
Tk nha!