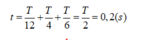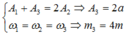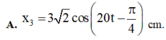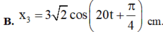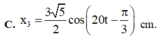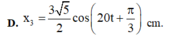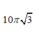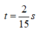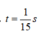Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án C
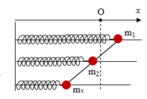
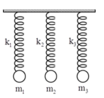
Ta có ω 1 = ω 2 = ω 3 = 10 π rad / s
Phương trình dao động của vật 1 và vật 2 là:
x 1 = 3 cos ( 10 πt - π 2 ) c m x 2 = 1 , 5 cos ( 10 πt ) ( n ế u q u y ư ớ c t ọ a đ ộ x = 1 , 5 = ± A )
Trong quá trình dao động cả ba vật nằm trên một đường thẳng khi 2 x 2 = x 1 + x 3 ⇒ x 3 = 2 x 2 - x 1
tính chất trung bình
Bấm máy tính tổng hợp dao động ta được
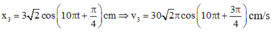
Taị t = 0 và v 30 = - 30 π cm / s
Trường hợp x 2 = 1 , 5 cos ( 10 π t + π ) ( n ế u q u y ư ớ c t ọ a đ ộ x = 1 , 5 = - A )
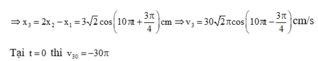


Tại thời điểm t = 0 để ba dao động này thẳng hàng thì
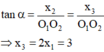
→ dễ thấy rằng chỉ có A và B là phù hợp.
+ Tương tự như vậy, sau khoảng thời gian 0,25T, m1 đến biên, m2 trở vè vị trí cân bằng. Để ba vật thẳng hàng thì
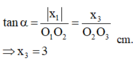
Tại thời điểm t = 0 vật có li độ x3 = 3 cm sau đó 0,25T vật vẫn có li độ x3 = 3 cm → tại t = 0 vật chuyển động theo chiều dương → φ0 = 0,25π.
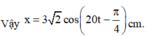
Đáp án A

Đáp án D
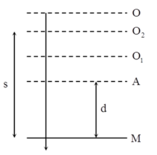
Gọi O1 là vì trí cân bằng của lò xo nếu không có giá đỡ
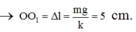
Giá đỡ M chuyển động nhanh dần đều hướng xuống ® lực quán tính F hướng lên.
+ Gọi vị trí cân bằng mới là O2 thì
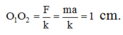
® OO2 = 4 cm.
+ Khi giá đỡ xuống tới O2 thì vật và giá đỡ tách ra nên:
* Vận tốc của vật và giá đỡ tại O2 là:
![]() m/s
m/s
* Li độ của vật là: x = - 1 cm
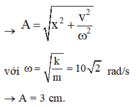
Thời gian vật đi từ vị trí x = -1 cm đến A = 3 cm tương ứng với góc j là
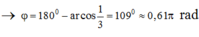
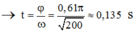
Quãng đường giá đỡ M đi được từ O2 trong thời gian trên là:
![]()
d = S - O2A = 7,2 - 4 = 3,2 cm » 3 cm

Đáp án A
+ Ta tính được
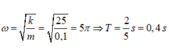
+ Độ biến dạng của lò xo khi vật ở vị trí cân bằng là
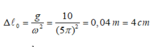
+ Từ VTCB, nâng vật lên 2 cm, tức là vật cách vị trí cân bằng 2 cm, suy ra |x| = 2 cm.
Áp dụng hệ thức liên hệ ta tính được biên độ dao động
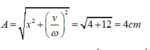
+ Sơ đồ chuyển động của vật được minh họa trên hình vẽ. Từ đó thay thấy thời điểm mà lúc vật qua vị trí lò xo dãn 6 cm lần hai (ở li độ x = 2 cm lần hai) là