TL
2
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
12 tháng 10 2017
a) Ta có y tỉ lệ thuận với x theo hệ số tỉ lệ k nên y = kx mà khi x = 5 thì y = 3.
Suy ra: 3=k.5⇒k=353=k.5⇒k=35
b) y=35xy=35x
c) Khi x = -5 thì y=35.(−5)=−3y=35.(−5)=−3
Khi x = 10 thì y=35.10=6y=35.10=6
TN
7 tháng 12 2017
a,Theo bài ra, ta có: y tỉ lệ thuận với x theo hệ số tỉ lệ là k(k hằng số khác 0)
=>y=kx
Với x=5,y=3 thì 3=k5
=>k=\(\dfrac{3}{5}\)
Vậy y tỉ lệ thuận với x theo hệ số tỉ lệ là \(\dfrac{3}{5}\)
b,Khi k=\(\dfrac{3}{5}\)mà ta lại có y=kx
=>y=\(\dfrac{3}{5}\)x
Vậy y=\(\dfrac{3}{5}\)x
c,Với x=-5=>y=\(\dfrac{3}{5}\).(-5)=-3
Với x=10=>y=\(\dfrac{3}{5}\).10=6
Vậy với x=10,y=6 và với x=-5,y=-3
TP
28 tháng 8 2017
Đồ thị hàm số đi qua O (0; 0)
Cho x = 2 ⇒ y = 1,5. 2 = 3
Ta có: A(2; 3)
Vẽ đường thẳng OA ta có đồ thị hàm số.
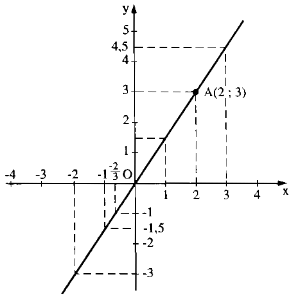
a) f(1) = 1,5. 1 = 1,5
f(-1) = 1,5. (-1) = -1,5
f(-2) = 1,5. (-2) = -3
f(2) = 1,5. 2 = 3
f(0) =0
b)\(y=-1\Rightarrow x=\dfrac{-1}{1,5}=-\dfrac{2}{3}\)
\(y=0\Rightarrow x=\dfrac{0}{1,5}=0\)
\(y=4,5\Rightarrow x=\dfrac{4,5}{1,5}=3\)
c) y > 0 ⇒1,5x > 0 ⇒x > 0
y < 0 ⇒ 1,5x < 0 ⇒ x < 0
TP
28 tháng 8 2017
Đồ thị hàm số đi qua O (0; 0)
Cho x = 2 ⇒⇒ y = 1,5. 2 = 3
Ta có: A(2; 3)
Vẽ đường thẳng OA ta có đồ thị hàm số.
a) f(1) = 1,5. 1 = 1,5
f(-1) = 1,5. (-1) = -1,5
f(-2) = 1,5. (-2) = -3
f(2) = 1,5. 2 = 3
f(0) = 0
b)y=−1⇒x=\(\dfrac{-1}{1,5}=-\dfrac{2}{3}\)
b)y=0⇒x==\(\dfrac{0}{1,5}=0\)
y=4,5⇒x=\(\dfrac{4,5}{1,5}=3\)
c) y > 0 ⇒1,5x > 0 ⇒x > 0
y < 0 ⇒ 1,5x < 0 ⇒ x < 0
LH
18 tháng 4 2017
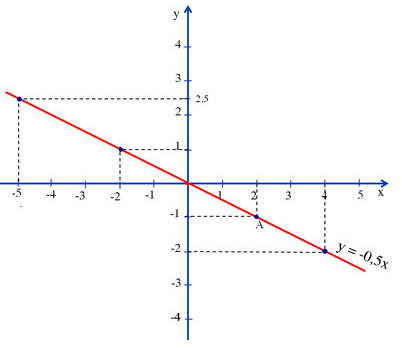
Cho x =2 được y =-2 =>A(2 ;-1) thuộc đồ thị. Vẽ đồ thị
a) Trên đồ thị ta thấy
f(2)=-1
f(-2) =1
f(4)=-2
f(0)=0;
b) Trên đồ thị ta thấy
y=-1 => x=2
y=0 => x=0
y=2,5 => x=-5
c) Khi y dương y > 0 ứng với phần đồ thị nằm trên trục hoành và bên trái trục tung nên x < 0.
Khi y âm : y < 0 ứng với phần đồ thị nằm trên trục hoành và bên phải trục tung nên x > 0
23 tháng 1 2017
Đặt \(\frac{x-1}{2}=\frac{y+3}{4}=\frac{z-5}{6}=k\)
=> x = 2k + 1
y = 4k - 3
z = 6k + 5
Thay vào biểu thức 5z - 3x - 4y = 50 , ta có :
5z - 3x - 4y = 50
=> 5.(6k + 5) - 3.(2k + 1) - 4.(4k - 3) = 50
=> 30k + 25 - (6k + 3) - (16k - 12) = 50
=> 30k + 25 - 6k - 3 - 16k + 12 = 50
=> (30k - 6k - 16k) + (25 - 3 + 12) = 50
=> 8k + 34 = 50
=> 8k = 16
=> k = 2
=> \(\hept{\begin{cases}x=2k+1=2.2+1=5\\y=4k+3=4.2+3=11\\z=6k+5=6.2+5=17\end{cases}}\)
b)
Đặt \(\frac{x}{2}=\frac{y}{3}=\frac{z}{4}=k\)
=> x = 2k
y = 3k
z = 4k
Thay vào biểu thức M , ta có :
\(M=\frac{y+z-x}{x-y+z}=\frac{3k+4k-2k}{2k-3k+4k}=\frac{5k}{3k}=\frac{5}{3}\)
9 tháng 6 2017
a) Vì x và y là hai đại lượng tỉ lệ thuận, nên :
y = ax (a là hệ số tỉ lệ, a khác 0)
Khi đó : \(\begin{cases} y_1 = ax_1\\ y_2 = ax_2 \end{cases}\)
Suy ra \(y_1+y_2=a\left(x_1+x_2\right)\) => -10 = a.2 => a = -5
Vậy : y = -5x
b) y = 5
2x + 624 = 5x
624 = 5x - 2x
Vì x ϵ N nên ta có thể lập bảng sau:
Khi x > 5 thì 5x - 2x bằng 3093 hoặc lớn hơn nên giá trị trên không thể bằng 624. Còn khi 0 ≤ x < 5 thì không có giá trị nào của x ϵ N thì giá trị bằng 624.
Do đó không có giá trị x ϵ N thõa mãn đề bài.
2\(^x\) + 624 = 5\(y\)
Nếu \(x\) = 0 ta có: 20 + 624 = 5y
5y = 625
5y = 54
y = 4
Nếu \(x\) > 0 ⇒ 2\(x\) + 624 ⋮ 2 ∀ \(x\) \(\in\) N
2\(^x\) + 624 = 5y ⇒ 5y ⋮ 2 (vô lý)
vì 5y = 1 hoặc 5y = \(\overline{..5}\) không chia hết cho 2 ∀ y
Vậy \(x\) = 0 và y = 4 là nghiệm duy nhất thỏa mãn đề bài