MD
1
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
NL
1
QA
2
AL
27 tháng 12 2017
P thuộc Z <=> (2n1-1) chia hết cho (n-1)
<=> (2n-2+1) chia hết cho (n-1)
<=> [(2n-2)+1] chia hết cho (n-1)
<=> [2(n-1)+1] chia hết cho (n-1)
Vì 2(n-1) chia hết cho (n-1)
=> P thuộc Z <=> 1 chia hết cho n-1
<=> n-1 thuộc Ư(1)
<=> n-1=1
hoặc n-1=-1
<=> n=2
hoặc n=0
Vậy P thuộc Z <=> n thuộc {2;0}
Thấy đúng nhớ k cho mình nha
27 tháng 12 2017
Ta có : \(\frac{2n-1}{n-1}=\frac{2}{n-1}.\frac{n-1}{n-1}=\frac{2}{n-1}.1\)
Vì \(1\in Z\)nên \(\frac{2}{n-1}\in Z\)
\(\Rightarrow n-1\in\)Ư(2)
Ư(2) = { -2;-1;1;2}
Ta có bảng sau :
| n-1 | -2 | -1 | 1 | 2 |
| n | -1 | 0 | 2 | 3 |
Vậy \(n\in\left\{-1;0;2;3\right\}\)
NA
1
25 tháng 12 2017
Ta có: P = \(\frac{2n-1}{n-1}=\frac{2n-2+1}{n-1}=\frac{2\left(n-1\right)+1}{n-1}=2+\frac{1}{n-1}\)
Để \(\frac{2n-1}{n-1}\)là số nguyên thì\(\frac{1}{n-1}\)là số nguyên
\(\Rightarrow\)\(n-1\inƯ\left(1\right)=\left\{1;-1\right\}\)
Vậy để \(\frac{2n-1}{n-1}\)là số nguyên thì \(n\in\left\{1;-1\right\}\)
VH
20 tháng 12 2018
Đặng Thu Trang ko phải vậy đâu mik đánh xong bài rùi nhưng nó mất đâu ý chứ mik ko bị thần kinh đâu
KT
3 tháng 1 2018
\(\frac{1}{2}a=\frac{2}{3}b=\frac{3}{4}c\)
\(\Leftrightarrow\)\(\frac{a}{12}=\frac{b}{9}=\frac{c}{8}\)
Ap dụng tính chất dãy tỉ số bằng nhau ta có:
\(\frac{a}{12}=\frac{b}{9}=\frac{c}{8}=\frac{a-b}{12-9}=\frac{15}{3}=5\)
suy ra \(\hept{\begin{cases}\frac{a}{12}=5\\\frac{b}{9}=5\\\frac{c}{8}=5\end{cases}}\)\(\Leftrightarrow\)\(\hept{\begin{cases}a=60\\b=45\\c=40\end{cases}}\)
Vậy.....
LD
3 tháng 1 2018
Áp dụng tính chất dãy tỉ số bằng nhau ta có:
\(\frac{a}{2}=\frac{2b}{3}=\frac{3c}{4}=\frac{a}{2}=\frac{b}{\frac{3}{2}}=\frac{3c}{4}=\frac{a-b}{2-\frac{3}{2}}=\frac{15}{\frac{1}{2}}=30\)
\(\Rightarrow\)\(\hept{\begin{cases}\frac{a}{2}=30\Rightarrow a=60\\\frac{2b}{3}=30\Rightarrow b=45\\\frac{3c}{4}=30\Rightarrow c=40\end{cases}}\)
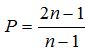
Để P là số nguyên thì \(n-1\in\left\{1;-1\right\}\)
hay \(n\in\left\{2;0\right\}\)