Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) Ta có :
\(BC^2=AB^2+AC^2\left(Pitago\right)\)
\(\Leftrightarrow AC^2=BC^2-AB^2=169-25=144\)
\(\Leftrightarrow AC=12\left(cm\right)\)
\(\dfrac{1}{AH^2}=\dfrac{1}{AB^2}+\dfrac{1}{AC^2}\)
\(\Leftrightarrow\dfrac{1}{AH^2}=\dfrac{AB^2.+AC^2}{AB^2.AC^2}\)
\(\Leftrightarrow\dfrac{1}{AH^2}=\dfrac{BC^2}{\left(AB.AC\right)^2}\)
\(\Leftrightarrow AH^2=\dfrac{\left(AB.AC\right)^2}{BC^2}=\dfrac{\left(5.12\right)^2}{13^2}\)
\(\Leftrightarrow AH=\dfrac{5.12}{13}=\dfrac{60}{13}\sim4,85\left(cm\right)\)
\(sin\widehat{B}=\dfrac{AC}{BC}=\dfrac{12}{13}\Rightarrow\widehat{B}\sim67^o\)
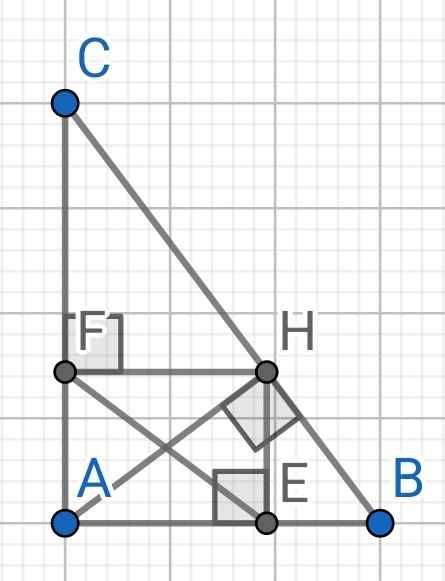 a) ∆ABC vuông tại A (gt)
a) ∆ABC vuông tại A (gt)
BC² = AB² + AC² (Pytago)A
⇒ AC² = BC² - AB²
= 13² - 5²
= 144
⇒ AC = 12 (cm)
Ta có:
AH.BC = AB.AC
⇒ AH = AB.AC : BC
= 5.12 : 13
= 60/13 (cm) ≈ 4,62 (cm)
sinB = AC/BC = 12/13
⇒ ∠B ≈ 67⁰
b) ∆AHB vuông tại H có HE là đường cao
⇒ HE² = AE . EB (1)
∆AHC vuông tại H có HF là đường cao
⇒ HF² = AF . FC (2)
Tứ giác AEHF có:
∠AEH = ∠EAF = ∠AFH = 90⁰
⇒ AEHF là hình chữ nhật
⇒ AH = EF
⇒ ∠EHF = 90⁰
∆EHF vuông tại H
⇒ EF² = HE² + HF²
⇒ AH² = HE² + HF²
Từ (1) và (2)
⇒ AE.EB + AF.FC = HE² + HF² = AH²
∆ABC vuông tại A vó AH là đường cao
⇒ AH² = HB.HC
⇒ AE.EB + AF.FC = HB.HC
⇒ AE.EB + AF.FC - HB.HC = 0
c) AH = EF đã chứng minh ở câu b

1: ΔABC vuông tại A
=>\(AB^2+AC^2=BC^2\)
=>\(AC^2+9=36\)
=>\(AC^2=27\)
=>\(AC=3\sqrt{3}\left(cm\right)\)
Chu vi tam giác ABC là:
\(3+3\sqrt{3}+6=9+3\sqrt{3}\left(cm\right)\)
Xét ΔABC vuông tại A có AH là đường cao
nên \(AH\cdot BC=AB\cdot AC\)
=>\(AH\cdot6=3\cdot3\sqrt{3}=9\sqrt{3}\)
=>\(AH=\dfrac{3\sqrt{3}}{2}\left(cm\right)\)
2:
a: Xét tứ giác AEHF có
\(\widehat{AEH}=\widehat{AFH}=\widehat{FAE}=90^0\)
=>AEHF là hình chữ nhật
=>EF=AH
b: Xét ΔHAB vuông tại H có HE là đường cao
nên \(EA\cdot EB=HE^2\)
ΔHAC vuông tại H có HF là đường cao
nên \(FA\cdot FC=HF^2\)
\(EA\cdot EB+FA\cdot FC\)
\(=HE^2+HF^2=EF^2\)

Câu 1:
a: Xét ΔAHB vuông tạiH có HD là đường cao
nên \(AD\cdot AB=AH^2\left(1\right)\)
Xét ΔAHC vuông tại H có HE là đường cao
nên \(AE\cdot AC=AH^2\left(2\right)\)
Từ (1) và (2) suy ra \(AD\cdot AB=AE\cdot AC\)
b: \(BC=\sqrt{4^2+6^2}=2\sqrt{13}\left(cm\right)\)
\(AH=\dfrac{4\cdot6}{2\sqrt{13}}=\dfrac{12}{\sqrt{13}}\left(cm\right)\)
\(AE=\dfrac{AH^2}{AC}=\dfrac{144}{13}:6=\dfrac{24}{13}\left(cm\right)\)

a.Xét ΔABC vuông tại A có:
+AB²+AC²=BC²(Pytago)
⇔AC²=BC²-AB²
⇔AC²=6²-3²=27
⇔AC=3√3(cm)
+sinB=AC/BC(Định nghĩa tỉ số lượng giác)
⇔sinB=3√3/6
⇒B=60°
+/B+C=90°
⇒C=90°-B=30°
b.Xét ΔABC vuông tại A có:
AH.BC=AC.AB(Hệ thức về cạnh và góc trong tam giác vuông)
⇔AH=AC.AB/BC
⇔AH=3√3.5/6≈4,33(cm)
Xét tứ giác AEHF có:
A=AEH=AFH(=90°)
⇒AEHF là hình chữ nhật(dhnb)
⇒EF=AH(tính chất hcn AEHF)
c.Xét ΔABH vuông tại H:
HE²=EB.EA(Hệ thức về cạnh và góc trong tam giác vuông) (1)
Xét ΔAHC vuông tại H :
HF²=AF.FC(Hệ thức về cạnh và góc trong tam giác vuông) (2)
Vì AEHF là hcn (cmb)
⇒EHF=90°(t/c)
Xét ΔHEF vuông tại H có:
HE²+HF²=EF²(pytago) (3)
Từ (1),(2) và (3)⇒EA.EB+AF.FC=EF²
⇒EA.EB+AF.FC=AH²(AH=EF)
⇒EA.EB+AF.FC≈4,33²≈18,7489

a: ΔABC vuông tại A
=>\(BC^2=AB^2+AC^2\)
=>\(BC=\sqrt{6^2+8^2}=10\left(cm\right)\)
Xét ΔABC vuông tại A có AH là đường cao
nên \(AH\cdot BC=AB\cdot AC\)
=>\(AH\cdot10=6\cdot8=48\)
=>AH=4,8cm
Xét ΔABC vuông tại A có \(sinACB=\dfrac{AB}{BC}=\dfrac{3}{5}\)
=>\(\widehat{ACB}\simeq36^052'\)
b: ΔHAB vuông tại H có HE là đường cao
nên \(AE\cdot AB=AH^2\left(1\right)\)
ΔHAC vuông tại H có HF là đường cao
nên \(AF\cdot AC=AH^2\left(2\right)\)
Từ (1),(2) suy ra \(AE\cdot AB=AF\cdot AC\)
=>\(\dfrac{AE}{AC}=\dfrac{AF}{AB}\)
Xét ΔAEF vuông tại A và ΔACB vuông tại A có
\(\dfrac{AE}{AC}=\dfrac{AF}{AB}\)
Do đó: ΔAEF đồng dạng với ΔACB
=>\(\widehat{AFE}=\widehat{ABC}\)

b: Xét tứ giác ADHE có
\(\widehat{ADH}=\widehat{AEH}=\widehat{EAD}=90^0\)
Do đó: ADHE là hình chữ nhật
Suy ra: AH=DE

Bạn tự vẽ hình.
(a) \(BC^2=AB^2+AC^2\left(Pythagoras\right)\)
\(\Rightarrow AC=\sqrt{BC^2-AB^2}=\sqrt{5^2-3^2}=4\left(cm\right)\)
+) \(sinB=\dfrac{AC}{BC}=\dfrac{4}{5}\Rightarrow\hat{B}\approx53^o\)
+) \(\hat{C}=90^o-\hat{B}\approx90^o-53^o=37^o\)
(b) +) \(AB.AC=BC.AH\Leftrightarrow AH=\dfrac{AB.AC}{BC}=\dfrac{3\cdot4}{5}=2,4\left(cm\right)\)
\(\hat{A}=\hat{E}=\hat{F}=90^o\left(gt\right)\Rightarrow AEHF\) là hình chữ nhật.
Do đó, \(EF=AH\left(đpcm\right)\)