Question

[Nguyễn Xuân Thành]

Cho tam giác ABC ( AB<AC) , tia phân giác của góc A cắt cạnh BC tại D . Gọi M là trung điểm của cạnh BC, qua M kẻ đường thẳng // với AD, đường thẳng này cắt tia đối của AB tại E và cắt cạnh AC tại F. C/M: BE=FC

Answer 1

[Nguyễn Thị Thương Hoài]

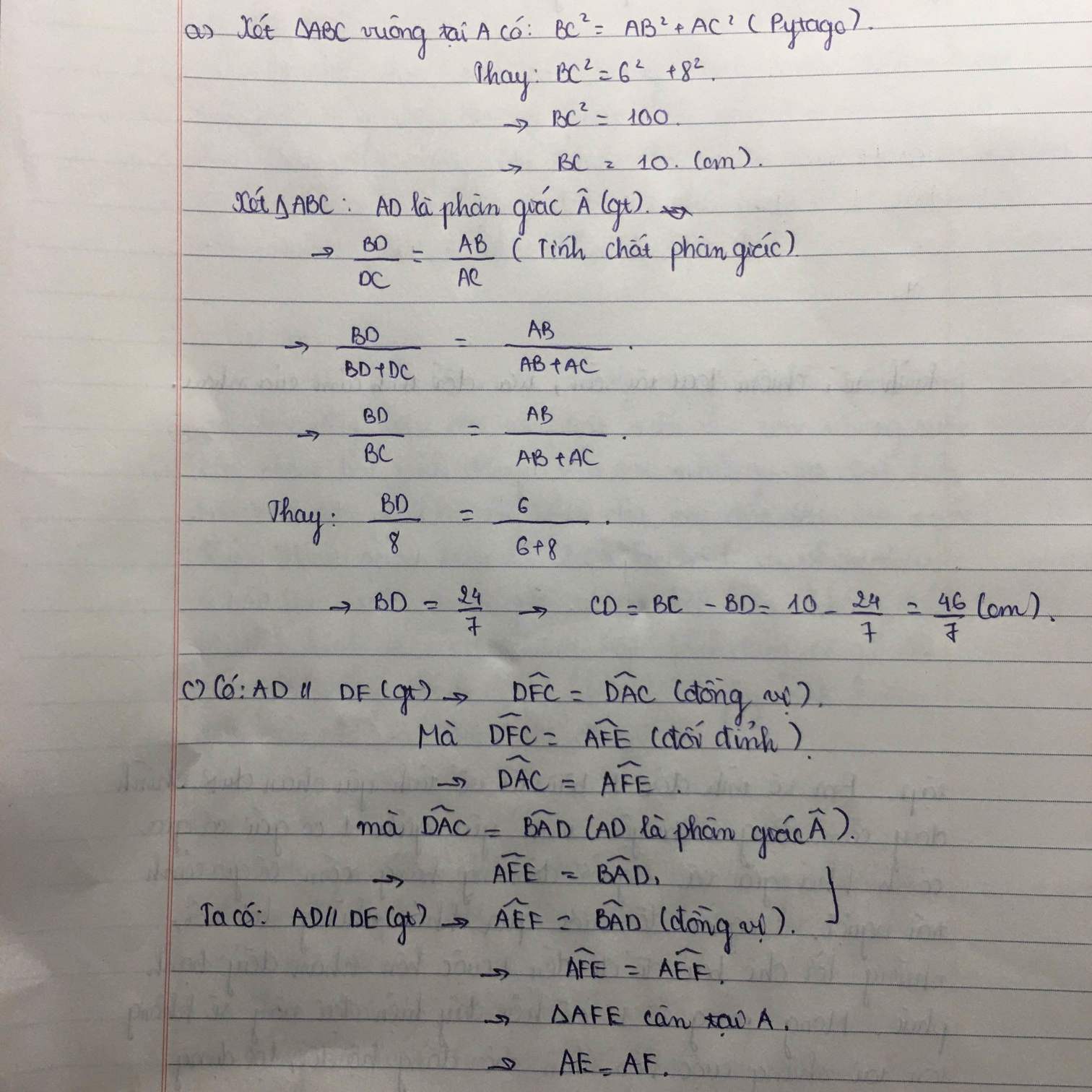
Kéo dài AC về phía A lấy điểm H sao cho CF = FH;

Lúc này bài toán trở thành chứng minh BE = HF

Xét tam giác HBC có: MB = MC (gt); FH = FC 

Nên MF là đường trung bình của tam giác HBC ⇒ ME//BH

Mặt khác ta có ME//AD ⇒  \(\widehat{AEF}\) = \(\widehat{BAD}\) (hai góc đồng vị) (1)

                                    \(\widehat{BAD}\) = \(\widehat{DAF}\) (AD là phân giác của góc BAC) (2) 

                                      \(\widehat{DAF}\) = \(\widehat{AFE}\) (hai góc so le trong)  (3)

Kết hợp (1);(2);(3) ta có: \(\widehat{AEF}\) = \(\widehat{AFE}\) ⇒ \(\Delta\)AEF cân tại A ⇒ AE = AF (*)

Vì ME//HB nên: \(\widehat{AHB}\) = \(\widehat{AFE}\) (so le trong)

                         \(\widehat{ABH}\) = \(\widehat{AEF}\) (so le trong)

          ⇒   \(\widehat{AHB}\) = \(\widehat{ABH}\) ⇒ \(\Delta\) AHB cân tại A ⇒ AB = AH (**)

Cộng vế với vế của(*) và(*) ta có: AE + AB = AF + AH  

                                 ⇒ BE = FH

                                  ⇒ BE = CF (vì cùng bằng HF)