Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

\(u_1=a.\cos\left(wt\right)\)
\(u_2=a.cos\left(wt+\pi\right)\)
Nhận thấy A và B là nguồn ngược pha.
Gọi M là trung điểm của A và B => \(d_1=AM\Rightarrow d_2=BM\)
Biên độ giao động tại M :
\(A_M=\left|2a\cos\left(\frac{\varphi_1-\varphi_2}{2}+\frac{\pi\left(d_2-d_1\right)}{\lambda}\right)\right|\)
\(\Rightarrow A_M=\left|2a\sin\frac{\pi\left(d_1-d_2\right)}{\lambda}\right|\)
Mà d1 = d2
=> AM =0

Bạn lưu ý, là bài này khác bài kia là A sớm pha hơn B nhé.
Do A sớm pha hơn B là \(\frac{\pi}{2}\) nên tương tự bài trước, mình lấy điểm A' cùng pha với B.
Do đó, A'A = \(\frac{\lambda}{4}\)
Điểm M dao động biên độ cực tiểu khi: \(d_2-\left(d_1-\frac{\lambda}{4}\right)=\left(k+\frac{1}{2}\right)\lambda\Rightarrow d_2-d_1=\left(k+\frac{1}{4}\right)\lambda\)
Theo đáp án, ta có: \(d_2-d_1=-1,75cm=\left(-2+\frac{1}{4}\right)\lambda\)
Nên M dao động cực tiểu.

Suy ra được bạn nhé, vì:
Giả sử:
\(\begin{cases}u_1=A_1\cos\left(\omega t\right)\\u_2=\pm A_2\cos\left(\omega t\right)\end{cases}\)\(\Rightarrow\begin{cases}v_1=-\omega A_1\sin\left(\omega t\right)\\v_2=\mp\omega A_2\cos\left(\omega t\right)\end{cases}\)\(\Rightarrow\frac{v_1}{v_2}=\pm\frac{A_1}{A_2}\)
(Dấu + ứng với 2 dao động cùng pha, dấu - ứng với dao động ngược pha)

Điểm A sớm pha hơn B là: \(\frac{2}{3}\pi\)
Điểm M dao động với biên cực đại khi: \(d_2-\left(d_1-\frac{\lambda}{3}\right)=k\lambda\Rightarrow d_2-d_1=k\lambda-\frac{\lambda}{3}\)
Giả sử M lệch phía A, cách trung điểm AB là x thì:\(d_2-d_1=\frac{AB}{2}+x-\left(\frac{AB}{2}-x\right)=2x=k\lambda-\frac{\lambda}{3}\)
\(\Rightarrow x=\frac{k\lambda}{2}-\frac{\lambda}{6}\)
Nhận thấy xmin khi k = 0 \(\Rightarrow x_{min}=-\frac{\lambda}{6}\)
Dấu "-" chứng tỏ x lệch về phía ngược lại mà tả đã giả sử, là phía B.

Đề nghị bạn gửi mỗi bài một câu thôi, nhìn thế này hoa mắt quá :)
1. Chu kì sóng: \(T=\frac{2\pi}{\omega}=\frac{2\pi}{4\pi}=0,5s\)
Bước sóng: \(\lambda=v.T=12.0,5=6m\)
Độ lệch pha giữa 2 điểm: \(\Delta\varphi=\frac{2\pi d}{\lambda}=\frac{2\pi.1,5}{6}=\frac{\pi}{2}\)

A B M d1 d2 B'
Mình giải thích chi tiết hơn công thức của bạn Giang Nam thế này:
B sớm pha hơn A là \(\frac{\pi}{3}\)
Mình lấy điểm B' trên phương truyền sóng BM sao cho B' cùng pha với A, nên B' trễ pha \(\frac{\pi}{3}\)so với B \(\Rightarrow BB'=\frac{\lambda}{6}\)
B' cùng pha với A nên B dao động cực đại thì: \(MB'-MA=k\lambda\Leftrightarrow\left(d_2-\frac{\lambda}{6}\right)-d_1=k\lambda\)
\(\Leftrightarrow d_2-d_1=k\lambda+\frac{\lambda}{6}\)(Trong công thức của bạn Giang Nam phải sửa lại như thế này mới đúng đc)
Dựa theo các phương án của bài toán thì d1=12cm, d2 = 18cm thỏa mãn công thức trên nên điểm M dao động biên cực đại.

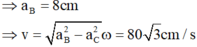
Vì là sóng dọc nên phương dao động trùng phương truyền sóng.
O A B 20 42 u1 u2
Chọn O là gốc tọa độ, trong quá trình dao động tọa độ của A, B lần lượt là:
\(\begin{cases}x_A=20+u_1\\x_B=42+u_2\end{cases}\)
Khoảng cách giữa 2 điểm là: \(\Delta x=x_B-x_A=\left(42+u_2\right)-\left(20+u_1\right)=22+\left(u_2-u_1\right)=22-10\cos\left(\omega t\right)\)
Do đó, khoảng cách max giữa 2 điểm là: 22+ 10 = 32 cm.