Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Chọn C
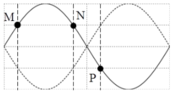
+ M và N cùng pha, do đó M và N cùng nằm trên một bó. Dựa vào các biên độ các vị trí đặt biệt trên dây khi xảy ra sóng dừng, ta xác định được các điểm M, N và P dao động với biên độ bằng một nửa biên độ bụng.
+ Tốc độ của bụng khi sợi dây duỗi thẳng vmax = ωA = 80 cm/s

Đáp án A
M, N dao động ngược pha, có cùng biên độ nên M, N đối xứng với nhau qua một nút.
M, N, P cùng biên độ nên ta giả sử N, P đối xứng qua bụng A.
Độ lệch pha biên độ dao động tại M, P là π.
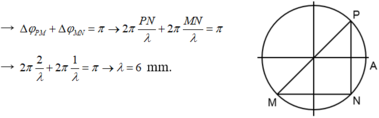
Độ lệch pha biên độ dao động tại N và bụng là 2π.1/6 = π/3.
→ Biên độ A = 8 mm.
Lại có T = 0,08 s → ω = 78,5 → v = Aω = 628 mm/s.

chọn đáp án D
Xét khoảng cách từ một điểm tới nút gần nhất có khoảng cách là d( với
d
<
λ
4
)
ta có •
d
=
λ
12
thì biên độ dao động tại điểm đó là
A
2
•
d
=
λ
8
thì biên đọ dao động tại điểm đó là
A
2
2
d
=
λ
6
thì biên độ tại điểm đó là
A
3
2
Với A là biên độ dao động tại bụng sóng
►Đây là tb tự luận :P
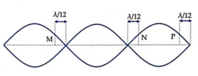
Xét ba điểm M N P liên tiếp nhau trên một sợi dây mang sóng dừng
Ta có M và N dao động ngược pha nhau nên M và N đối xứng nhau qua một nút
M,N, P là ba điểm liên tiếp cùng biên độ nên ta có N và P đối xứng nhau qua một bụng
Biểu diễn trên hình ta có
M
N
2
+
N
P
2
=
λ
4
⇒
λ
=
6
c
m
GỌi M và N đối xứng nhau qua nút O
Xét Pt sóng tới O
u
1
=
A
cos
(
ω
t
)
Sóng phản xạ tại O
u
2
=
A
cos
(
ω
t
+
π
)
Xét tại điểm N
=
2
A
cos
(
π
2
+
2
π
O
N
λ
)
cos
(
ω
t
+
π
2
)
Biên độ sóng tại N
A
N
=
2
A
/
cos
(
π
2
+
2
π
O
N
λ
)
/
⇒
2
A
=
8
c
m
Như vậy biên độ tại bụng là 8 mm
Khoảng thời gian giữa hai lần sợi dây duỗi thẳng là
T
2
=
0
,
04
⇒
T
=
0
,
4
s
Vận tốc cực đại của phần tử tại bụng sóng
v
=
A
ω
=
A
2
π
T
=
628
m
m
/
s

Đề nghị bạn gửi mỗi bài một câu thôi, nhìn thế này hoa mắt quá :)
1. Chu kì sóng: \(T=\frac{2\pi}{\omega}=\frac{2\pi}{4\pi}=0,5s\)
Bước sóng: \(\lambda=v.T=12.0,5=6m\)
Độ lệch pha giữa 2 điểm: \(\Delta\varphi=\frac{2\pi d}{\lambda}=\frac{2\pi.1,5}{6}=\frac{\pi}{2}\)


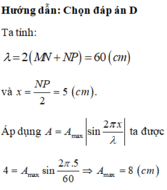

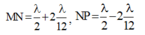
Suy ra được bạn nhé, vì:
Giả sử:
\(\begin{cases}u_1=A_1\cos\left(\omega t\right)\\u_2=\pm A_2\cos\left(\omega t\right)\end{cases}\)\(\Rightarrow\begin{cases}v_1=-\omega A_1\sin\left(\omega t\right)\\v_2=\mp\omega A_2\cos\left(\omega t\right)\end{cases}\)\(\Rightarrow\frac{v_1}{v_2}=\pm\frac{A_1}{A_2}\)
(Dấu + ứng với 2 dao động cùng pha, dấu - ứng với dao động ngược pha)
Hay quá.