
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.



\(-\frac{2005}{2010}< \frac{2001}{2002}\) vì \(-\frac{2005}{2010}\) là số âm còn \(\frac{2001}{2002}\) là số dương, mà số dương lúc nào cũng lớn hơn số âm

a.\(\frac{13}{17}\)=1-\(\frac{4}{17}\); \(\frac{46}{50}\)=1-\(\frac{4}{50}\)
Vì \(\frac{4}{17}\)>\(\frac{4}{50}\)=> 1-\(\frac{4}{17}\)<1-\(\frac{4}{50}\)
Vậy\(\frac{13}{17}\)<\(\frac{46}{50}\)

Vì \(\frac{2000}{2001}< \frac{2003}{2002}\) do \(\frac{2000}{2001}< 0< \frac{2003}{2003}\) (tử lớn hơn mẫu) nên khi là số nguyên âm \(\frac{2000}{-2001}>\frac{-2003}{2002}\)

Có : A = 2002^2 = 2002.2002 = (2001+1).(2002 = 2001.2002+2002 = (2001.2002+2001)+1 = 2001.(2002+1)+1 = 2001.2003+1>2001.2003
=> A > B
k mk nha


Đầu tiên bạn đi chứng minh bài toán:a>b thì \(\frac{a}{b}>\frac{a+m}{b+m}\)
rồi áp dụng vào bài toán này
\(\frac{2^{2006}+7}{2^{2004}+7}>\frac{2^{2006}+7+1}{2^{2004}+7+1}=\frac{2^{2006}+8}{2^{2004}+8}=\frac{2^3\left(2^{2003}+1\right)}{2^3\left(2^{2001}+1\right)}=\frac{2^{2003}+1}{2^{2001}+1}\)
Vậy \(\frac{2^{2006}+7}{2^{2004}+7}>\frac{2^{2003}+1}{2^{2001}+1}\)
Đấy thế là xong!
A B C D 30 m 675 m^2 E
Đặt các điểm như hình trên thì AB = 0,6 CD ; AB + 30 m = CD (BE = 30 m) ; SABCD + 675 m2 = SAECD (SBEC = 675 m2)
AECD là hình chữ nhật nên CE là đường cao tam giác BEC ; CE = AD
=> AD = 2 x SBEC : BE = 2 x 675 : 30 = 45 (m)
AB + 30 m = CD mà AB = 0,6 CD nên 0,6 CD + 30 m = CD => 0,4 CD = 30 m => CD = 75 m => AB = 45 m
=> SABCD = (AB + CD) x AD : 2 = (75 + 45) x 45 : 2 = 2700 (m2)
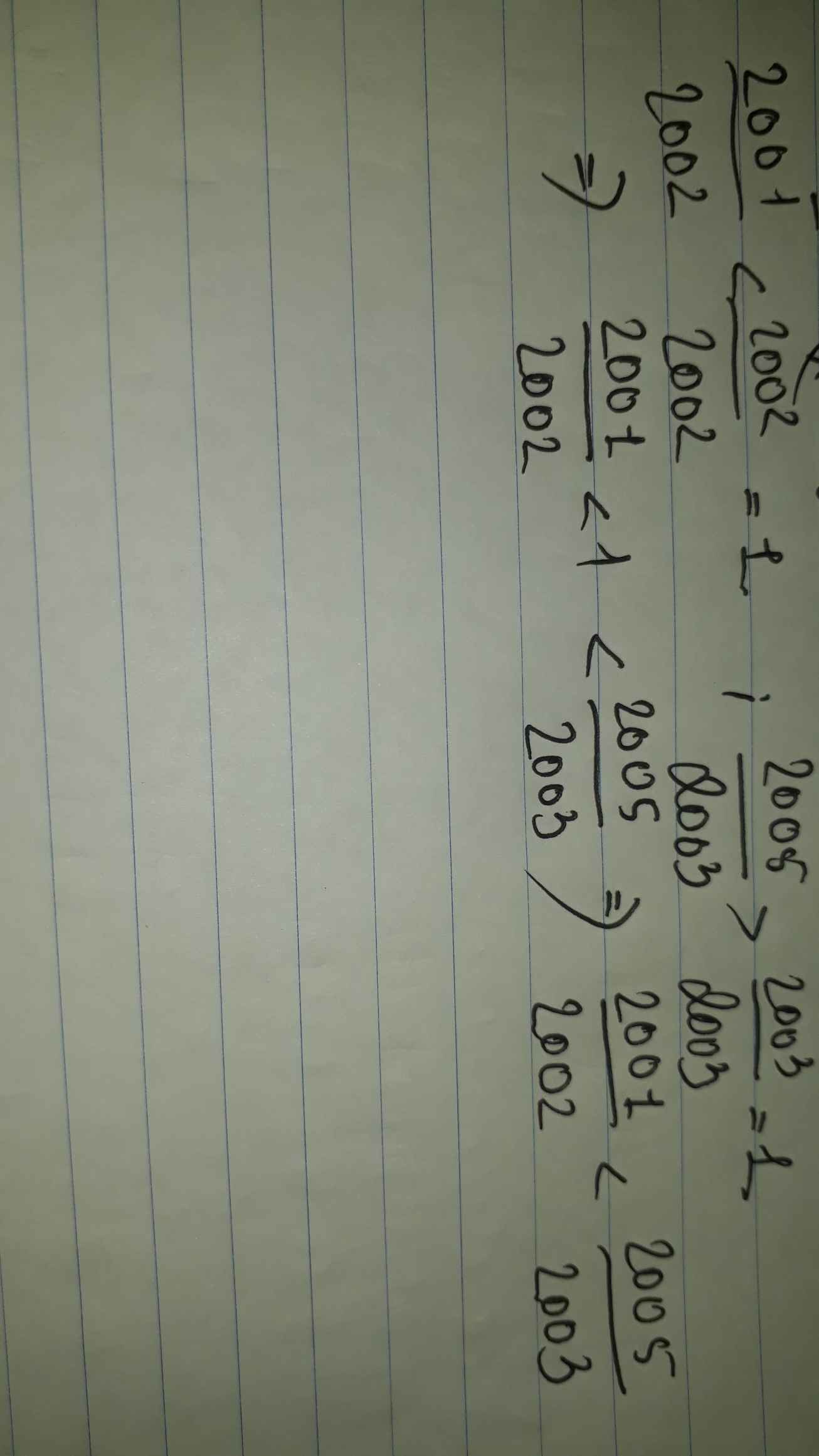
2001/2001<2005/2003 vì 2001/2001=1 mà 2005/2003 >1 Vậy 2001/2001<2005/2003
Có \(\frac{2001}{2001}=1=\frac{2003}{2003}\)
Mà \(\frac{2003}{2003}< \frac{2005}{2003}\)
=>\(\frac{2001}{2001}< \frac{2005}{2003}\)