Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) \(\sqrt{\left(2-\sqrt{3}\right)^2}+\sqrt{4-2\sqrt{3}}\)
= \(2-\sqrt{3}+\sqrt{\left(\sqrt{3}-1\right)^2}\)
\(2-\sqrt{3}+\sqrt{3}-1\) = \(1\)
b) \(\sqrt{15-6\sqrt{6}}+\sqrt{33-12\sqrt{6}}\)
= \(\sqrt{\left(3-\sqrt{6}\right)^2}+\sqrt{\left(3-2\sqrt{6}\right)^2}\)
= \(3-\sqrt{6}+2\sqrt{6}-3\) = \(\sqrt{6}\)
c) \(\left(15\sqrt{200}-3\sqrt{450}+2\sqrt{50}\right):\sqrt{10}\)
= \(\dfrac{15\sqrt{200}}{\sqrt{10}}-\dfrac{3\sqrt{450}}{\sqrt{10}}+\dfrac{2\sqrt{50}}{\sqrt{10}}\)
= \(15\sqrt{20}-3\sqrt{45}+2\sqrt{5}\)
= \(30\sqrt{5}-9\sqrt{5}+2\sqrt{5}\) = \(23\sqrt{5}\)

Bài 1:
a: \(=\sqrt{\dfrac{7-4\sqrt{3}}{2-\sqrt{3}}}\cdot\sqrt{2+\sqrt{3}}\)
\(=\sqrt{2-\sqrt{3}}\cdot\sqrt{2+\sqrt{3}}=1\)
Bài 2:
\(VT=\left(4+\sqrt{15}\right)\cdot\left(\sqrt{5}-\sqrt{3}\right)\cdot\sqrt{8-2\sqrt{15}}\)
\(=\left(4+\sqrt{15}\right)\left(8-2\sqrt{15}\right)\)
\(=32-8\sqrt{15}+8\sqrt{15}-30=2\)

\(A=\left(4+\sqrt{15}\right)\left(\sqrt{5}-\sqrt{3}\right)\sqrt{8-2\sqrt{15}}\)
\(A=\left(4+\sqrt{15}\right)\left(\sqrt{5}-\sqrt{3}\right)\sqrt{\left(\sqrt{5}-\sqrt{3}\right)^2}\)
\(A=\left(4+\sqrt{15}\right)\left(\sqrt{5}-\sqrt{3}\right)^2\)
\(A=\left(4+\sqrt{15}\right)\left(8-2\sqrt{15}\right)\)
\(A=2\left(4+\sqrt{15}\right)\left(4-\sqrt{15}\right)=2\)
\(B=\sqrt{6-2\sqrt{5}}\left(\sqrt{5}-1\right)\left(3+\sqrt{5}\right)\)
\(B=\sqrt{\left(\sqrt{5}-1\right)^2}\left(\sqrt{5}-1\right)\left(3+\sqrt{5}\right)\)
\(B=\left(\sqrt{5}-1\right)^2\left(3+\sqrt{5}\right)\)
\(B=\left(6-2\sqrt{5}\right)\left(3+\sqrt{5}\right)=2\)

a/ \(=\frac{\sqrt{4+2\sqrt{3}}}{\sqrt{2}}-\frac{\sqrt{4-2\sqrt{3}}}{\sqrt{2}}=\frac{\sqrt{\left(\sqrt{3}+1\right)^2}-\sqrt{\left(\sqrt{3}-1\right)^2}}{\sqrt{2}}=\frac{\sqrt{3}+1-\sqrt{3}+1}{\sqrt{2}}=\frac{2}{\sqrt{2}}=\sqrt{2}\)
b/ \(=\frac{\left(8+2\sqrt{15}\right)}{2}.\left(\sqrt{5}-\sqrt{3}\right)\sqrt{8-2\sqrt{15}}\)
\(=\frac{\left(\sqrt{5}+\sqrt{3}\right)^2}{2}.\left(\sqrt{5}-\sqrt{3}\right)\sqrt{\left(\sqrt{5}-\sqrt{3}\right)^2}\)
\(=\frac{\left(\sqrt{5}+\sqrt{3}\right)^2}{2}.\left(\sqrt{5}-\sqrt{3}\right)\left(\sqrt{5}-\sqrt{3}\right)\)
\(=\frac{\left(\sqrt{5}+\sqrt{3}\right)^2}{2}.\left(\sqrt{5}-\sqrt{3}\right)^2=\frac{\left(5-3\right)^2}{2}=2\)

câu E dễ nhất nên mình làm trước , các câu còn lại làm tương tự ( biến đổi thành hằng đẳng thức rồi rút gọn ) :
\(E=\sqrt{9-2.3.\sqrt{6}+6}+\sqrt{24-2.2\sqrt{6}.3+9}\)
\(=\sqrt{\left(3-\sqrt{6}\right)^2}+\sqrt{\left(2\sqrt{6}-3\right)^2}\)
\(=\left|3-\sqrt{6}\right|+\left|2\sqrt{6}-3\right|\)
\(=3-\sqrt{6}+2\sqrt{6}-3\) ( vì \(3-\sqrt{6}>0;2\sqrt{6}-3>0\) )
\(=\sqrt{6}\)
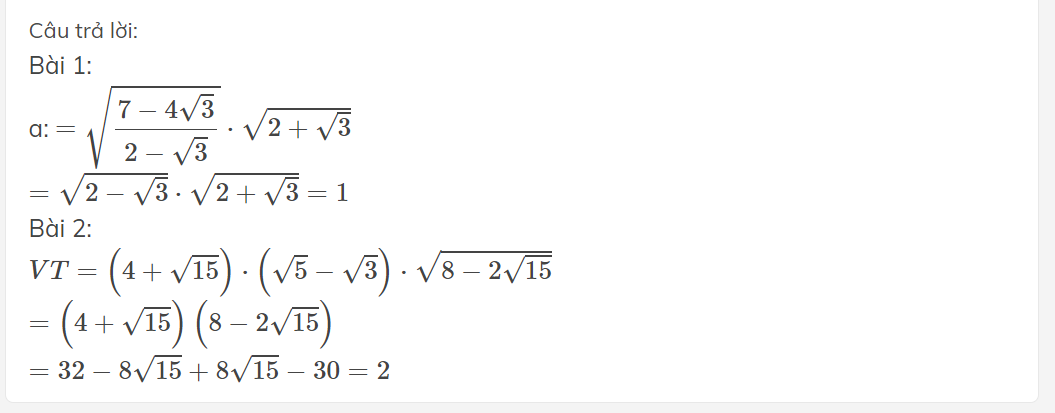
a,A.√2= √(4+2√3)-√(4-2√3)
= √(1+√3)2 -√( √3 -1)2
= 1+√3-√3+1= 2
=> A= 2/√2=√2
B2= (4+√15)2.(4-√15).(√10-√6)2
= (4+√15).1.(16-4√15)
= (4+√15).(4-√15).4
= 4
=> B = √4 = 2