Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


11)11) 3x(x-5)2-(x+2)3+2(x-1)3-(2x+1)(4x2-2x+1)=3x(x2-10x+25)-(x3+6x2+12x+8)+2(x3-3x2+3x-1)-(8x3+1)=3x3-30x2+75x-x3-6x2-12x-8+2x3-6x2+6x-2-8x3-1=-4x3-42x2+63x-11

Câu 1 (2,0 điểm) Thực hiện phép tính:
a) 2xy.3x2y3
b) x.(x2 - 2x + 5)
c) (3x2 - 6x) : 3x
d) (x2 – 2x + 1) : (x – 1)
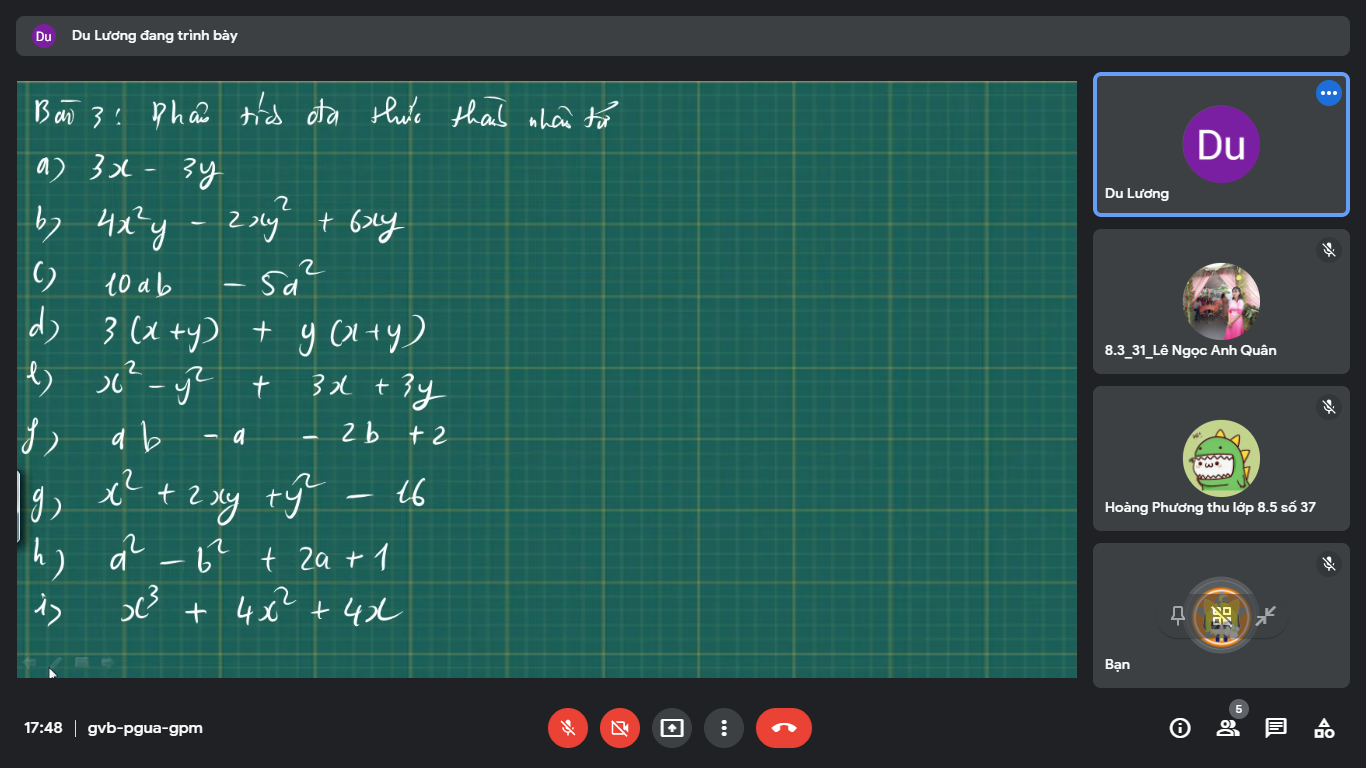
Câu 2 (2,0 điểm). Phân tích các đa thức sau thành nhân tử:
a) 5x2y - 10xy2
b) 3(x + 3) – x2 + 9
c) x2 – y2 + xz - yz
Câu 3 (2,0 điểm). Cho biểu thức:
a) Với điều kiện nào của x thì giá trị của biểu thức A được xác định?
b) Rút gọn biểu thức A.
c) Tìm giá trị của biểu thức A tại x = 1.
Câu 4 (3,5 điểm). Cho tam giác MNP vuông tại M, đường cao MH. Gọi D, E lần lượt là chân các đường vuông góc hạ từ H xuống MN và MP.
a) Chứng minh tứ giác MDHE là hình chữ nhật.
b) Gọi A là trung điểm của HP. Chứng minh tam giác DEA vuông.
c) Tam giác MNP cần có thêm điều kiện gì để DE = 2EA.
Câu 5 (0,5 điểm). Cho a + b = 1. Tính giá trị của các biểu thức sau:
M = a3 + b3 + 3ab(a2 + b2) + 6a2b2(a + b).
Tk ủng hộ mk nha .
#Thiên_Hy

a: AN+CN=AC
=>AN=20-15=5cm
Xét ΔABC có AM/AB=AN/AC
nên MN//BC
b: Xét ΔAMN và ΔNPC có
góc AMN=góc NPC(=góc B)
góc ANM=góc NCP)
=>ΔAMN đồng dạng với ΔNPC


a) Xét ∆AND và ∆CMB có:
BM=DN (giả thiết)
AD=BC(các cạnh đối bằng nhau)
góc ADN=góc CBM( so le trong)
Vậy ∆AND=∆CMB( cạnh góc cạnh)
=> AN=CM( 2 cạnh tương ứng)( điều phải chứng minh)
b)AN//CM( góc ANM= góc CMN so le trong)và AN=CM( chứng minh trên)
=> Tứ giác AMCN là hình bình hành(điều phải chứng minh)
c)AN//CM mà N thuộc AI và M thuộc CK
->AI//CK
AB//DC mà K thuộc AB và I thuộc DC
->AK//DI
Vậy tứ giác AKCI là hình bình hành( các cạnh đối song song)
=> AC và KI là đường chéo của hình bình hành AKCI
=> AO= OC; KO=OI ( hai đường chéo cắt nhau tại trung điểm mỗi đường)
Vậy K,O,I cùng nằm trên cùng 1 đường thẳng( điều phải chứng minh)
hok tốt

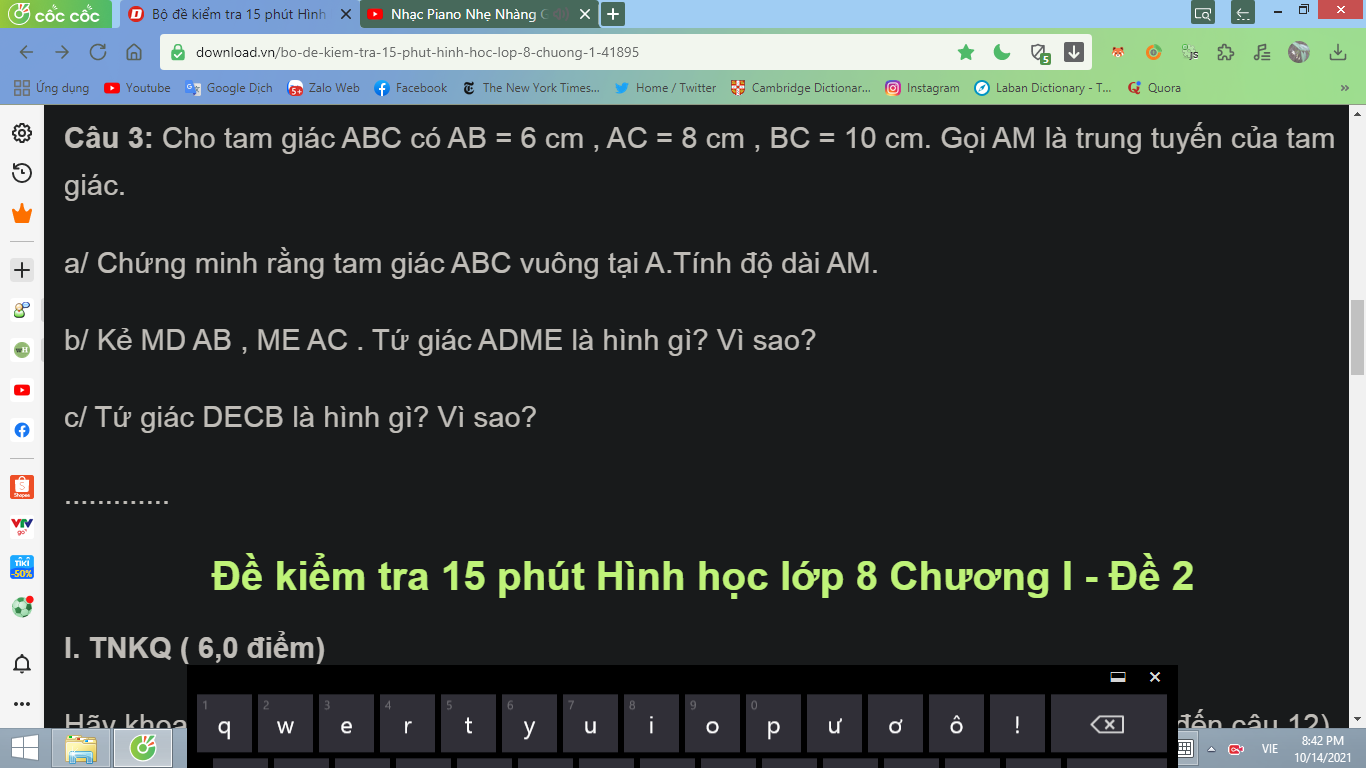
a: Xét ΔABC có \(BC^2=AB^2+AC^2\)
hay ΔABC vuông tại A
Ta có: ΔABC vuông tại A
mà AM là đường trung tuyến ứng với cạnh huyền BC
nên \(AM=\dfrac{BC}{2}=\dfrac{10}{2}=5\left(cm\right)\)


\(a,3x-3y=3\left(x-y\right)\\ b,4x^2y-2xy^2+6xy=2xy\left(2x-y+3\right)\\ c,10ab-5a^2=5a\left(2b-a\right)\\ d,3\left(x+y\right)+y\left(x+y\right)=\left(x+y\right)\left(3+y\right)\\ e,x^2-y^2+3x+3y=\left(x-y\right)\left(x+y\right)+3\left(x+y\right)=\left(x+y\right)\left(x-y+3\right)\\ f,ab-a-2b+2=a\left(b-1\right)-2\left(b-1\right)=\left(a-2\right)\left(b-1\right)\)
\(g,x^2+2xy+y^2-16=\left(x+y\right)^2-4^2=\left(x+y+4\right)\left(x+y-4\right)\\ h,a^2-b^2+2a+1=\left(a^2+2a+1\right)-b^2=\left(a+1\right)^2-b^2=\left(a+b+1\right)\left(a-b+1\right)\\ i,x^3+4x^2+4=x\left(x^2+4x+4\right)=x\left(x+2\right)^2\)

a,
Xét Δ ABH và Δ CBA, có :
\(\widehat{ABH}=\widehat{CAB}\) (góc chung)
\(\widehat{AHB}=\widehat{CAB}=90^o\)
=> Δ ABH ~ Δ CBA (g.g)
=> \(\dfrac{AB}{CB}=\dfrac{BH}{BA}\)
=> \(AB^2=BH.BC\)
Xét Δ ABC vuông tại A, có :
\(BC^2=AB^2+AC^2\) (Py - ta - go)
=> \(BC^2=15^2+20^2\)
=> BC = 25 (cm)
Ta có : \(AB^2=BH.BC\) (cmt)
=> \(15^2=BH.25\)
=> BH = 9 (cm)
Ta có : BC = BH + CH
=> 25 = 9 + CH
=> CH = 16 (cm)
b,
Xét Δ AMN và Δ ACB, có :
\(\widehat{MAN}=\widehat{CAB}=90^o\)
\(\widehat{MAN}=\widehat{CAB}\) (góc chung)
=> Δ AMN ~ Δ ACB (g.g)
=> \(\dfrac{AM}{AC}=\dfrac{AN}{AB}\)
=> AM.AB = AN.AC
Ta có : \(\dfrac{AM}{AC}=\dfrac{AN}{AB}\)
=> \(\dfrac{AB}{AC}=\dfrac{AN}{AM}\)
=> \(\dfrac{AN}{AM}=\dfrac{15}{20}=\dfrac{3}{4}\)
Vậy : ta có kết luận : Δ AMN = \(\dfrac{3}{4}\) Δ ACB