Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Áp dụng định li Py - ta - go vào △ ABC vuông tại C ta có:
AB2 = BC2 + AC2
AB2 = 122 + 52 = 169
⇒ AB = \(\sqrt{169}=13\)
Vậy cáp treo được xây dựng dài 13 km

Câu 1: Người ta muốn mắc dây điện từ một trạm biến áp A đến một khu dân cư B được xây dựng nằm cách xa nhau tại hai bờ của một con sông d. Vị trí trên bờ sông để cắm cột mắc dây C sao cho số mét dây phải dùng là ngắn nhất là:
A. Vị trí cắm cột C là chân đường vuông góc hạ từ trạm biến áp A đến bờ sông d.
B. Vị trí cắm cột C là chân đường vuông góc hạ từ một vị trí B của khu dân cư đến bờ sông d.
C. Vị trí cắm cột C là giao điểm của AB và bờ sông d.
D. Vị trí cắm cột C bất kì trên bờ sông d.

a: Khoảng cách từ B đến C là 12-9=3(km)
b: Chi phí làm đường ống từ B đến C là
\(3\cdot5000=15000\left(USD\right)\)

Gọi x,y,z lần lượt là số tiền mỗi đơn vị phải trả, ta có x+y+z=340 (triệu)
Do số tiền tỉ lệ thuận với số xe và tỉ lệ nghịch với khoảng cách của mỗi đơn vị đến nơi xây cầu nên ta có;
x.1,5/8=y3/,6=z.1/4⇔x/8=y/3=z/6
Áp dụng tính chất dãy tỉ số bằng nhau ta có:
x/8=y/3=z/6=x+y+z/8+3+6=340/17=20
⇒x=20.8=160; y=20.3=60; z=6.20=120
Vậy số tiền mỗi đơn vị phải trả lần lượt là 160 triệu, 60 triệu và 120 triệu.

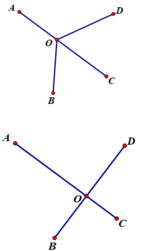
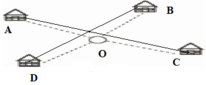
Gọi O là địa điểm đặt nhà máy (O tùy ý)
A, B, C, D lần lượt là bốn điểm dân cư (A,B, C, D cố định).
Ta luôn có:
OA + OC ≥ AC
OB + OD ≥ BD
⇒ OA + OB + OC + OD ≥ AC + BD (AC + BD là hằng số)
Vậy để OA + OB + OC + OD nhỏ nhất thì OA + OC = AC và OB + OD = BD.
OA + OC = AC khi O thuộc đoạn AC.
OB + OD = BD khi O thuộc đoạn BD.
Vậy OA + OB + OC + OD nhỏ nhất khi O là giao điểm của hai đoạn AC và BD.