Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Câu 1: Người ta muốn mắc dây điện từ một trạm biến áp A đến một khu dân cư B được xây dựng nằm cách xa nhau tại hai bờ của một con sông d. Vị trí trên bờ sông để cắm cột mắc dây C sao cho số mét dây phải dùng là ngắn nhất là:
A. Vị trí cắm cột C là chân đường vuông góc hạ từ trạm biến áp A đến bờ sông d.
B. Vị trí cắm cột C là chân đường vuông góc hạ từ một vị trí B của khu dân cư đến bờ sông d.
C. Vị trí cắm cột C là giao điểm của AB và bờ sông d.
D. Vị trí cắm cột C bất kì trên bờ sông d.

a: Khoảng cách từ B đến C là 12-9=3(km)
b: Chi phí làm đường ống từ B đến C là
\(3\cdot5000=15000\left(USD\right)\)

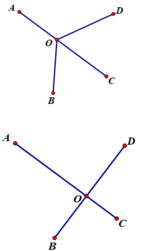
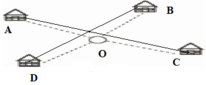
Gọi O là địa điểm đặt nhà máy (O tùy ý)
A, B, C, D lần lượt là bốn điểm dân cư (A,B, C, D cố định).
Ta luôn có:
OA + OC ≥ AC
OB + OD ≥ BD
⇒ OA + OB + OC + OD ≥ AC + BD (AC + BD là hằng số)
Vậy để OA + OB + OC + OD nhỏ nhất thì OA + OC = AC và OB + OD = BD.
OA + OC = AC khi O thuộc đoạn AC.
OB + OD = BD khi O thuộc đoạn BD.
Vậy OA + OB + OC + OD nhỏ nhất khi O là giao điểm của hai đoạn AC và BD.

Ta có:
\(AC+BC\ge AB\) ( vì \(C\)là điểm chưa xác định )
Do đó:
\(AC+BC\)ngắn nhất khi:
\(AC+BC=AB\)
\(\Rightarrow C\)nằm giữa \(AB\)
Vậy vị trí đặt một cột mắc dây điện từ trạm về cho khu dân cư sao cho độ dài đường dây ngắn nhất là \(C\)nằm giữa \(AB\)
Ta có: AC + BC ≥ AB ( vì C là điểm chưa xác định)
Do đó : AC + BC ngắn nhất khi:
AC + BC = AB
=> C nằm giữa A và B
Vậy vị trí đặt một cột mắc dây điện từ trạm về cho khu dân cư sao cho độ dài đường dây dẫn ngắn nhất là C nằm giữa A và B
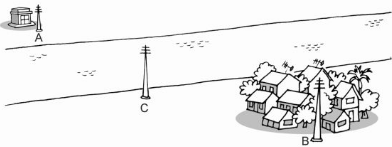
Áp dụng định li Py - ta - go vào △ ABC vuông tại C ta có:
AB2 = BC2 + AC2
AB2 = 122 + 52 = 169
⇒ AB = \(\sqrt{169}=13\)
Vậy cáp treo được xây dựng dài 13 km