Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Mạch LC có i vuông qua với q nên:
\((\dfrac{i}{I_0})^2+(\dfrac{q}{Q_0})^2=1\)\(\Rightarrow (\dfrac{i}{\omega Q_0})^2+(\dfrac{q}{Q_0})^2=1\)
\(\Rightarrow (\dfrac{i_1}{\omega Q_0})^2+(\dfrac{q_1}{Q_0})^2=1\)
\((\dfrac{i_2}{\omega Q_0})^2+(\dfrac{q_2}{Q_0})^2=1\)
\(\Rightarrow (\dfrac{i_1}{\omega })^2+(q_1)^2=(\dfrac{i_2}{\omega })^2+(q_2)^2\)
\(\Rightarrow \omega ^2=\dfrac{i_1^2-i_2^2}{q_2^2-q_1^2}\)
\(\Rightarrow T=\dfrac{2\pi}{\omega}=2\pi.\sqrt{\dfrac{q_2^2-q_1^2}{i_1^2-i_2^2}}\)
\(\Rightarrow \lambda = c.T =2\pi c.\sqrt{\dfrac{q_2^2-q_1^2}{i_1^2-i_2^2}}\)
Chọn B.

Bài này chỉ cần sử dụng công thức 2 giá trị của C để có cùng 1 giá trị của $U_C$ :
$U_C=U_{C_{max}} \cos \left(\dfrac{\varphi _1-\varphi _2}{2} \right)$
$\Rightarrow U_{C_{max}}=\dfrac{60}{\cos \dfrac{\pi }{6}}=40\sqrt{3} V$
Khi $U_{C_{max}}$ ta có:
$P=\dfrac{U^2}{R}\cos ^2\varphi _3=P_{max}\cos ^2\varphi _3=\dfrac{P_{max}}{2}$
$\Rightarrow \cos \varphi _3=\dfrac{\sqrt{2}}{2}$
Vẽ giản đồ suy ra: $U=\dfrac{U_{C_{max}}}{\sqrt{2}}=20\sqrt{6}\left(V \right)$

Dựa vào phương trình sóng => \(\lambda = 2 \pi (m), f = 50Hz\)
Tốc độ truyền sóng là \(v = \lambda.f=2\pi50= 100\pi (m/s)\)
Tốc độ cực đại của phần tử vật chất môi trường là \(v_{max}= A.w=3.100\pi (m/s)\)
\(\Rightarrow \frac{v}{v_{max}} = \frac{100\pi}{3.100\pi}=\frac{1}{3} \)

Do u và i dao động vuông pha => tại mọi thời điểm ta có
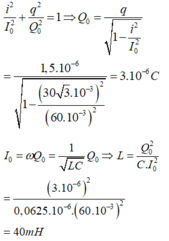
Đáp án B

- Do u và i dao động vuông pha ⇒ tại mọi thời điểm ta có:
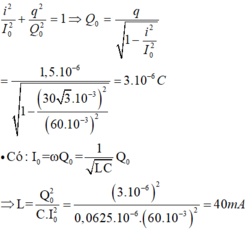

\(\lambda = v/f=20/50=0.4cm.\)
\( A_M = |2a\cos\pi(\frac{d_2-d_1}{\lambda}-\frac{\triangle\varphi}{2\pi})| = |2a\cos\pi(\frac{4,8-5,3}{0,4}-\frac{0}{2\pi})|=|2a\cos\frac{-5\pi}{4}|=\sqrt{2}a = 2\sqrt{2}\)
\( u_M = A_M\cos(2\pi ft - \pi\frac{d_2+d_1}{\lambda}+\frac{\varphi_1+\varphi_2}{2})=2\sqrt{2}\cos(40 \pi t - \pi\frac{5,3+4,8}{0,4}+\frac{0}{2}) = 2\sqrt{2}\cos(40 \pi t - \pi\frac{5,3+4,8}{0,4})\\ = 2\sqrt{2}\cos(40 \pi t - 25,25\pi)mm.\)

\(\lambda = v/f = 5cm.\)
\(\triangle \varphi = \frac{\pi}{2}.\)
Số cực đại trên đoạn AB thỏa mãn:
\(-AB < d_2-d_1 < AB \Rightarrow -AB < (k+\frac{\triangle\varphi)}{2 \pi}\lambda < AB \\ \Rightarrow -12 < (k+\frac{1}{4})\lambda < 12. \\ \Rightarrow -2,65 < k < 2,15 \\ \Rightarrow k = -2,-1,0,1,2.\)
Có 5 cực đại.
Số cực tiểu trên đoạn AB thỏa mãn:
\(-AB < d_2-d_1 < AB \Rightarrow -AB < (2k+1+\frac{\triangle\varphi}{\pi})\frac{\lambda}{2} < AB \\ \Rightarrow -12 < (2k +1 + 1/2)\lambda/2 < 12 \\ \Rightarrow -3,15 < k < 1,65 \\ \Rightarrow k = -3,-2,-1,0,1.\)
Có 5 cực tiểu.
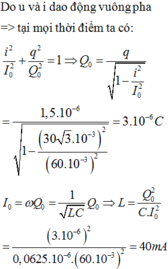
Do E và B biến thiên cùng pha nên, khi cảm ứng từ có độ lớn B0/2 thì điện trường E cũng có độ lớn E0/2.
Bài toán trở thành tính thời gian ngắn nhất để cường độ điện trường có độ lớn E0/2 đang tăng đến độ lớn E0/2.
E M N Eo Eo/2
Từ giản đồ véc tơ quay ta dễ dang tính được thời gian đó là t = T/3
Suy ra: \(t=\dfrac{5}{3}.10^{-7}\)s