Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Bài này chỉ cần sử dụng công thức 2 giá trị của C để có cùng 1 giá trị của $U_C$ :
$U_C=U_{C_{max}} \cos \left(\dfrac{\varphi _1-\varphi _2}{2} \right)$
$\Rightarrow U_{C_{max}}=\dfrac{60}{\cos \dfrac{\pi }{6}}=40\sqrt{3} V$
Khi $U_{C_{max}}$ ta có:
$P=\dfrac{U^2}{R}\cos ^2\varphi _3=P_{max}\cos ^2\varphi _3=\dfrac{P_{max}}{2}$
$\Rightarrow \cos \varphi _3=\dfrac{\sqrt{2}}{2}$
Vẽ giản đồ suy ra: $U=\dfrac{U_{C_{max}}}{\sqrt{2}}=20\sqrt{6}\left(V \right)$

Trong mạch dao động thì i sớm pha hơn q là \(\frac{\pi}{2}.\)

Do E và B biến thiên cùng pha nên, khi cảm ứng từ có độ lớn B0/2 thì điện trường E cũng có độ lớn E0/2.
Bài toán trở thành tính thời gian ngắn nhất để cường độ điện trường có độ lớn E0/2 đang tăng đến độ lớn E0/2.
E M N Eo Eo/2
Từ giản đồ véc tơ quay ta dễ dang tính được thời gian đó là t = T/3
Suy ra: \(t=\dfrac{5}{3}.10^{-7}\)s

Do u và i dao động vuông pha => tại mọi thời điểm ta có
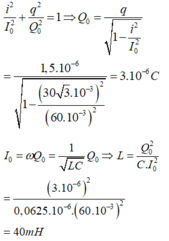
Đáp án B

- Do u và i dao động vuông pha ⇒ tại mọi thời điểm ta có:
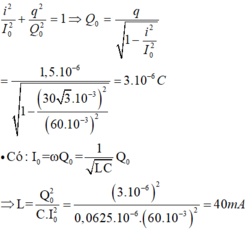

Khi C = C1 hoặc C = C2 thì I như nhau, do vậy:
\(Z_1=Z_2\Rightarrow Z_L-Z_{C1}=Z_{C2}-Z_L\Rightarrow Z_L=\dfrac{Z_{C1}+Z_{C2}}{2}=45\Omega\)
Để cường độ hiệu dụng qua R cực đại thì mạch xảy ra cộng hưởng.
\(\Rightarrow Z_C=Z_L=45\Omega\)
Chọn A.
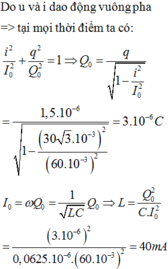
Mạch LC có i vuông qua với q nên:
\((\dfrac{i}{I_0})^2+(\dfrac{q}{Q_0})^2=1\)\(\Rightarrow (\dfrac{i}{\omega Q_0})^2+(\dfrac{q}{Q_0})^2=1\)
\(\Rightarrow (\dfrac{i_1}{\omega Q_0})^2+(\dfrac{q_1}{Q_0})^2=1\)
\((\dfrac{i_2}{\omega Q_0})^2+(\dfrac{q_2}{Q_0})^2=1\)
\(\Rightarrow (\dfrac{i_1}{\omega })^2+(q_1)^2=(\dfrac{i_2}{\omega })^2+(q_2)^2\)
\(\Rightarrow \omega ^2=\dfrac{i_1^2-i_2^2}{q_2^2-q_1^2}\)
\(\Rightarrow T=\dfrac{2\pi}{\omega}=2\pi.\sqrt{\dfrac{q_2^2-q_1^2}{i_1^2-i_2^2}}\)
\(\Rightarrow \lambda = c.T =2\pi c.\sqrt{\dfrac{q_2^2-q_1^2}{i_1^2-i_2^2}}\)
Chọn B.