Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

\(x=2\sin(\omega t +\dfrac{\pi}{2})=2\cos(\omega t)\) (cm)
Như vậy, ban đầu (t = 0) vật đang ở biên độ dương \(x=2cm\)
Khi quả cầu đi được nửa chu kì dao động thì nó sẽ lên biên độ âm, \(x=-2cm\)
Chiều dài lò xo: \(\ell=\ell_0+\Delta \ell_0+x=40+10-2=48(cm)\)

\(\omega=2\pi f = 9\pi (rad/s)\)
Biên độ \(A=(56-40)/2=8(cm)\)
Gốc thời gian lúc lò xo ngắn nhất --> biên độ (-A) -->\(\varphi=-\pi (rad)\)
Vậy: \(x=8\cos(9\pi t-\pi)(cm)\)
Chọn D.

Đáp án C
Phương pháp: Sử dụng lí thuyết về phương trình dao động điều hòa
Cách giải :
Vị trí cân bằng lò xo dãn một đoạn ∆ ε , ta có:
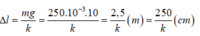
Vật được thả nhẹ từ vị trí lò xo dãn 6,5cm => biên độ dao động: A = 6,5 - 250 k
Vì A < 6,5cm nên dựa vào đáp án ta chọn A = 4cm
![]()
=> Phương trình dao động của vật: x = 4cos(20t) (cm)

Chọn đáp án D
A = l max − l min 2 = 56 − 40 2 = 8 ( c m ) ; ω = 2 π f = 10 π t
l C B = 56 − 8 = 48 ( c m )
Tại t = 0 ⇒ x = − 4 v < 0 ⇒ cos ϕ = − 1 2 sin ϕ > 0 ⇒ ϕ = 2 π 3
Vậy: x = 8 cos 10 π t + 2 π 3

Hướng dẫn:
+ Tần số góc của dao động ω = k m = 10 π rad/s.
Độ biến dạng của lò xo tại vị trí cân bằng Δ l 0 = m g k = 1 c m
+ Khi vật đang ở vị trí có li độ x = –1 cm → l = l 0 = 40 c m , người ta tiến hành giữ cố định lò xo tại điểm cách điểm cố định 20 cm → lò xo mới tham gia vào dao động có độ cứng k' = 2k = 200 N/m.
+ Năng lượng của con lắc trước khi cố định lò xo: E t = k x 2 = 0 , 01 E d = 1 2 k A 2 − x 2 = 0 , 035 J
→ Năng lượng của hệ sau cố định lò xo đúng bằng tổng động năng và một nửa thế năng của vật trước khi cố định lò xo.
E ' = 0 , 5 k A ' 2 = E d + 0 , 5 E t = 0 , 04 J → A' = 0,02 cm.
→ Lực đàn hồi cực đại F m a x = k ' ( 0 , 5 Δ l 0 + A ' ) = 6 N .
Đáp án B

Đáp án D
Chu kì dao động
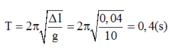
Trong một chu kì dao động, thời gian lò xo bị nén là khoảng thời gian vật đi từ x = ∆l đến x = A rồi trở về x = ∆l, tức là ∆t = 2t0 với t0 là thời gian đi từ x = ∆l đến x = A (giả sử chiều dương của trục tọa độ hướng lên).
Theo giả thiết:
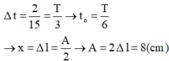
Khi lò xo giãn 8 cm ![]() vật đang chuyển động chậm dần đều nên đang đi ra biên, đi theo chiều dương hướng xuống
vật đang chuyển động chậm dần đều nên đang đi ra biên, đi theo chiều dương hướng xuống
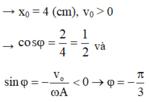
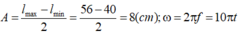
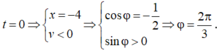
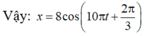
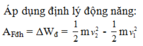
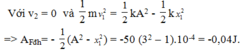

Ban đầu t = 0 thì x = 2 cm, lúc này vật đang ở biên độ dương.
Quả cầu dao động được nửa chu kì thì x = -2 cm (vật ở biên độ âm)
Chiều dài của lò xo: \(\ell=\ell_0+\Delta\ell_0+x=40+10-2=48(cm)\)