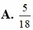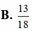Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Có 3 cách nhận quà: A.áo và sữa, B.áo và cặp, C.sữa và cặp
Gọi a;b;c lần lượt là số học sinh nhận quà thuộc 3 loại trên, ta có:
\(\left\{{}\begin{matrix}a+b+c=10\\a+b=7\\a+c=9\\b+c=4\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}a=6\\b=1\\c=3\end{matrix}\right.\)
Do có đúng 1 học sinh nhận được quà loại B nên Việt và Nam chỉ có thể nhận quà loại A hoặc C
Không gian mẫu: \(C_{10}^6C_4^3C_1^1\)
Số cách nhận thỏa mãn: \(C_8^4C_4^3C_1^1+C_{10}^6C_2^1C_1^1\)
Xác suất: \(P=\dfrac{C_8^4C_4^3C_1^1+C_{10}^6C_2^1C_1^1}{C_{10}^6C_4^3C_1^1}\)
Halo :D Ngày cuối cùng của năm 2020! Năm sau là năm con trâu rồi nhỉ, vậy thì.... chúc anh:
Hiền như trâu trẻ
Khỏe như trâu nhà
Và bla bla như trâu mộng :3
Chúc anh sớm có công việc ổn định, tìm được gf, và....hết rồi :)
P/s: Chúc trẻ rồi đấy nhá, đừng có kêu già này già nọ nữa nha anh :D

Chọn C
Chọn mỗi tổ hai học sinh nên số phần tử của không gian mẫu là ![]()
Gọi biến cố A: “Chọn 4 học sinh từ 2 tổ sao cho 4 em được chọn có 2 nam và 2 nữ”
Khi đó, xảy ra các trường hợp sau:
TH1: Chọn 2 nam ở Tổ 1, 2 nữ ở Tổ 2. Số cách chọn là ![]()
TH2: Chọn 2 nữ ở Tổ 1, 2 nam ở Tổ 2. Số cách chọn là ![]() .
.
TH3: Chọn ở mỗi tổ 1 nam và 1 nữ. Số cách chọn là ![]()
Suy ra, n(A) = ![]()
Xác suất để xảy ra biến cố A là: ![]()

Chọn C.
Giả sử số thứ tự trong danh sách là ![]()
Do dãy này là cấp số cộng nên ta có ![]()
![]() .
.
Số phần tử của không gian mẫu là n ( Ω ) = 10!
Gọi A là biến cố “Tổng các số thứ tự của hai em ngồi đối diện nhau là bằng nhau”. Để biến cố này xảy ra ta thực hiện liên tiếp các bước sau:
Bước 1: xếp thứ tự 5 cặp học sinh có các cặp số thứ tự là![]()
![]() vào trước 5 cặp ghế đối diện nhau. Bước này có 5! cách.
vào trước 5 cặp ghế đối diện nhau. Bước này có 5! cách.
Bước 2: xếp từng cặp một ngồi vào cặp ghế đối diện đã ) Chọn ở bước 1. Bước này có 2 5 cách.
Suy ra số kết quả thuận lợi cho biến cố A là 5!. 2 5 .
Vậy xác suất của biến cố A là ![]()

Chọn B.
Số phần tử của không gian mẫu:
![]()
Gọi A là biến cố “nhóm được chọn có cả nam và nữ, đồng thời mỗi khối có 1 học sinh nam”
⇒ số phần tử của biến cố A là: ![]()
![]() .
.