Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Chọn A.
Lời giải.
Không gian mẫu là số cách chọn 2 phần thưởng trong số 12 phần thưởng
Suy ra số phần tử của không gian mẫu là Ω = C 12 2 = 66
Gọi A là biến cố ""Bạn An và bạn Bình có phần thưởng giống nhau"".
Để tìm số phần tử của A, ta làm như sau
Gọi x là cặp số gồm 2 quyển Toán và Vật Lí
y là số cặp gồm 2 quyển Toán và Hóa Học;
z là số cặp gồm 2 quyển Vật Lí và Hóa Học
Ta có hệ phương trình
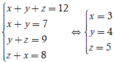
Suy ra số phần tử của biến cố A là
Ω A = C 3 2 + C 4 2 + C 5 2
Vậy xác suất cần tính P ( A ) = 19 66
Đáp án D
Ta chia số phần thưởng đó thành 3 bộ Toán Lý, 4 bộ Toán Hóa và 5 bộ Hóa Lý.
Như vậy, có C 12 2 cách chọn giải thưởng cho An và Bình
Trong đó, cách chọn số bộ Toán Lý là C 3 2 , cách chọn số bộ Toán Hóa là C 3 2 , cách chọn số bộ Hóa Lý là C 4 2
Do đó, xác suất là
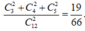
Đáp án D
Ta chia số phần thưởng đó thành 3 bộ Toán Lý, 4 bộ Toán Hóa và 5 bộ Hóa Lý.
Như vậy, có C 12 2 cách chọn giải thưởng cho An và Bình.
Trong đó, cách chọn số bộ Toán Lý là C 3 2
cách chọn số bộ Toán Hóa là C 4 2
cách chọn số bộ Hóa Lý là C 5 2 .
Do đó, xác suất là
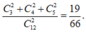
Chọn C
Xét phép thử T: “Chọn 7 cuốn sách từ 15 cuốn sách”.
Số phần tử của không gian mẫu trong phép thử là C 15 7 .
Gọi A biến cố chọn 7 cuốn sách có đủ 3 môn trong phép thử T.
Xác suất của biến cố cần tìm bằng xác suất của biến cố A.
Ta có 
Vậy
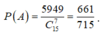
Đáp án là A.
• Ta tìm số cách chọn 7 cuốn còn lại sao cho không có đủ 3 môn.
Có 3 trường hợp :
• 7 cuốn còn lại gồm 2 môn toán lý : có C 9 7 cách
• 7 cuốn còn lại gồm 2 môn lý hóa : có C 11 7 cách
• 7 cuốn còn lại gồm 2 môn toán hóa : có C 10 7 cách
Suy ra có C 9 7 + C 11 7 + C 10 7 = 486 cách chọn 7 cuốn còn lại sao cho không có đủ 3 môn. Do đó số cách chọn 8 cuốn sao cho 7 cuốn còn lại có đủ 3 môn là C 15 7 - 486 = 5949 cách.
Xác suất cần tìm là P = 5949 C 15 7 = 661 715
Có 3 loại hình thức nhận thưởng: sách+sổ, sách+bút, sổ+bút
Gọi số học sinh nhận được phần thưởng thuộc 3 loại nói trên lần lượt là x;y;z
\(\Rightarrow\left\{{}\begin{matrix}x+y=9\\x+z=8\\y+z=11\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}x=3\\y=6\\z=5\end{matrix}\right.\)
Hay chúng ta có 3 bạn nhận thưởng sách+sổ, 6 bạn nhận sách+bút, 5 bạn nhận sổ+bút
Như vậy có 3 TH để An và Bình nhận thưởng giống nhau là:
- An Bình cùng nhận sách sổ: còn lại 12 bạn, chọn 6 bạn nhận sách bút có \(C_{12}^6\) sách, còn lại 6 bạn, chọn 5 bạn nhận sổ bút có \(C_6^5\) cách, còn 1 bạn, chọn 1 bạn nhận sách sổ có \(C_1^1\) cách \(\Rightarrow C_{12}^6.C_6^5.C_1^1\) cách
- An Bình nhận sách bút: tương tự như trên ta có \(C_{12}^3.C_9^4.C_5^5\) cách
- An Bình nhận bút sổ: \(C_{12}^3.C_9^6.C_3^3\) cách
Tổng: \(51744\) cách
Gọi a là số học sinh nhận được sách và sổ ; b là số học sinh nhận được sách và bút ; c là số học sinh nhận được sổ và bút. Ta có : \(a+b=9,a+c=8,b+c=11\)
Giải ra ta được \(a=3,b=6,c=5\)
Xét ba trường hợp sau : TH 1 : An và Bình cùng nhận được sách và sổ. Có 3 người cùng nhận được sách và sổ, trong đó có An và Bình. Vì vậy cần chọn ra 1 người trong só 12 học sinh để nhận sách và sổ suy ra có \(C_{12}^1\) cách chọn. Sau đó chọn ra 6 em trong số 11 học sinh còn lại để nhận sách và bút và 5 học sinh còn lại nhận sổ và bút. Vậy số kết quả trong TH này là: \(C_{12}^1.C^6_{12}\)
TH 2 : An và Bình cùng nhận được sách và bút. Lập luận tương tự TH 1 ta có số kết quả trong TH này là : \(C_{12}^4.C_8^3\)
TH 3 : An và Bình cùng nhận được sổ và bút. Số kết quả trong TH này là :\(C_{12}^3.C_9^3\). . Vậy có: \(C_{12}^1.C_{12}^6+C_{12}^4.C_8^3+C_{12}^3.C_9^3=51744\) cách phát phần thưởng thỏa mãn bài toán.
Đáp án: \(51744\)
Đáp án B
Gọi biến cố A: “Số cuốn sách còn lại của thầy Tuấn có đủ cả ba môn”.
Khi đó ta có biến cố: A ¯ : “Số cuốn sách còn lại của thầy Tuấn không có đủ cả 3 môn”.
`Loại 1: chọn tùy ý 7 cuôn từ 19 cuốn C719 = 50388 cách
Loại 2: chọn 7 cuốn từ 2 môn
TH1: hóa +lí : C711 = 330
TH2: lí+ toán: C714 = 3432
TH3: hóa+ toán: C713 = 1716
tổng = 5478
ta có: loại 1 - loại 2 = 50388-5478=44910( cách)
.
là VTCP của 2 đường thẳng d và d’. Nếu 
thì:
. Khi đó 
bằng:
. Tính 
. Khi đó:
.
. Tìm b.
.
. Tính 
.
và 
. Khi đó:
.
với 
.
và 
. Khi đó 
bằng:
. Khi đó 
bằng:
. Khi đó 
bằng
. Tính 
.