Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
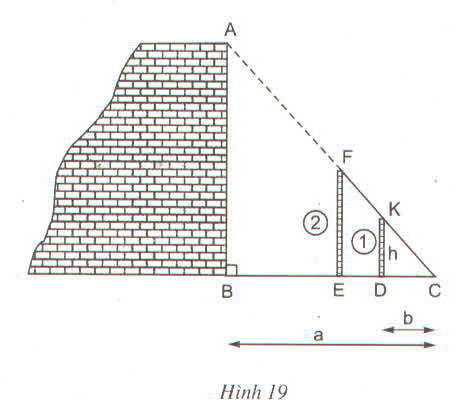
- Đặt hai cọc thẳng đứng, di chuyển cọc 2 sao cho 3 điểm A,F,K nằm trên đường thẳng.
- Dùng sợi dây căng thẳng qua 2 điểm F và K để xác định điểm C trên mặt đất( 3 điểm F,K,C thẳng hàng).
b) ∆BC có AB // EF nên EFABEFAB = ECBCECBC => AB = EF.BCECEF.BCEC = h.abh.ab
Vậy chiều cao của bức tường là: AB = h.abh.ab.
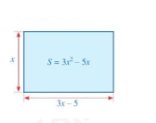
\(3{{\rm{x}}^2} - 5{\rm{x = x}}\left( {3{\rm{x}} - 5} \right)\)
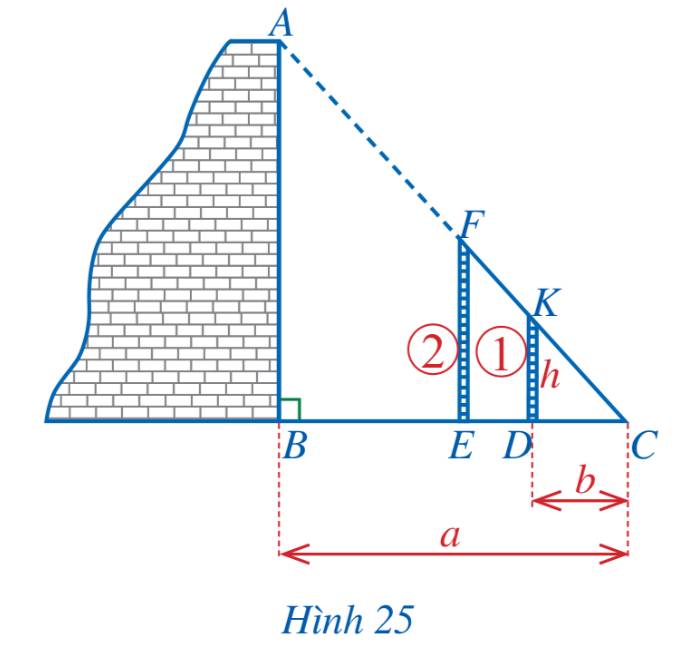
a) Cách tiến hành:
- Đặt hai cọc thẳng đứng, vuông góc với mặt đất sau đó di chuyển cọc 2 sao cho 3 điểm A, F, K thẳng hàng.
- Dùng sợi dây căng thẳng qua 2 điểm F và K để xác định điểm C trên mặt đất (3 điểm F, K, C thẳng hàng).
Sử dụng hệ quả của định lý Ta – let để tính chiều cao AB.
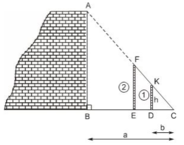
b) Ta có:
\(\left. \begin{array}{l}AB \bot BC\\DK \bot BC\end{array} \right\} \Rightarrow AB\parallel DK\)
Xét tam giác ABC với \(AB\parallel DK\) ta có:
\(\frac{{DK}}{{AB}} = \frac{{CD}}{{CB}}\) (Hệ quả của định lý Thales)
\( \Rightarrow AB = \frac{{DK.CB}}{{CD}} = \frac{{h.a}}{b}\).
a)
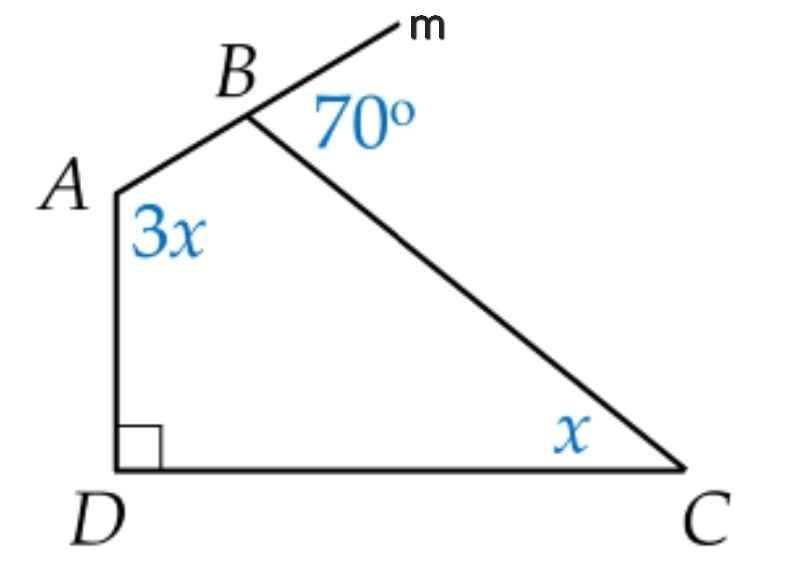Ta có:
∠ABC + ∠CBm = 180⁰ (kề bù)
⇒ ∠ABC = 180⁰ - ∠CBm
= 180⁰ - 70⁰
= 110⁰
Tứ giác ABCD có:
∠A + ∠ABC + ∠C + ∠D = 360⁰ (tổng bốn góc trong tứ giác ABCD)
⇒ 3x + 110⁰ + x + 90⁰ = 360⁰
⇒ 4x + 200⁰ = 360⁰
⇒ 4x = 360⁰ - 200⁰
4x = 160⁰
⇒ x = 160⁰ : 4
⇒ x = 40⁰
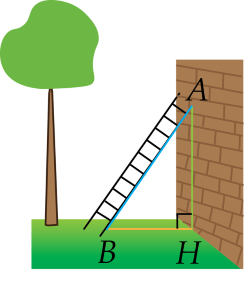
b) ∆ABH vuông tại H
⇒ AB² = AH² + BH² (Pytago)
⇒ AH² = AB² - BH²
= 3,7² - 1,2²
= 12,25
⇒ AH = 3,5
⇒ AH/BH = 3,5/1,2 ≈ 2,9 > 2,2
Vậy thang cách chân tường không "an toàn"
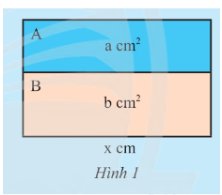
a) Cách 1: Chiều rộng hình chữ nhật lớn là: \(\left( {a + b} \right):x = \dfrac{{a + b}}{x}\) (cm)
Cách 2: Chiều rộng của hình chữ nhật A là: \(a:x = \dfrac{a}{x}\) (cm)
Chiều rộng của hình chữ nhật B là: \(b:x = \dfrac{b}{x}\) (cm)
Chiều rộng của hình chữ nhật lớn là: \(\dfrac{a}{x} + \dfrac{b}{x} = \dfrac{{a + b}}{x}\) (cm)
b) Chiều rộng của B lớn hơn chiều rộng của A là: \(\dfrac{a}{x} - \dfrac{b}{x} = \dfrac{{a - b}}{x}\) (cm)
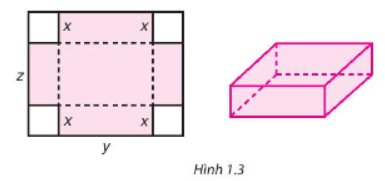
Hình gấp được là hình hộp chữ nhật có:
Chiều rộng là \(z - 2x\) (centimet)
Chiều dài là \(y - 2x\) (centimet)
Chiều cao là \(x\) (centimet)
Thể tích chiếc hộp là: \(\left( {z - 2x} \right).\left( {y - 2x} \right).x = \left( {zy - 2xz - 2xy + 4{x^2}} \right).x = xyz - 2{x^2}z - 2{x^2}y + 4{x^3}\) ( centimet khối)
Đa thức này có bậc là 3.
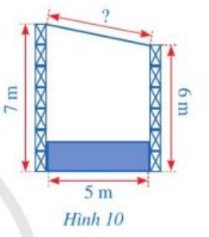
Gọi CB là chiều dài của mái che sân khấu. AB = 7- 6 = 1m, AC = 5m.
Từ C kẻ đường thẳng vuông góc với khung trước của sân khấu tại A. Ta có \( \Delta ABC \) vuông tại A.
Áp dụng định lí Pythagore trong tam giác vuông tại A. ta có:
\(C{B^2} = A{C^2} + A{B^2} = {1^2} + {5^2} = 26 \Rightarrow CB = \sqrt {26} = 5,10(m)\)
Áp dụng định lí Py-ta-go, ta có:
\(2,1^2+h^2=3,5^2\\ \Leftrightarrow h=\sqrt{3,5^2-2,1^2}=2,8m\)
a) Cách tiến hành:
- Đặt hai cọc thẳng đứng, di chuyển cọc 2 sao cho 3 điểm A, F, K nằm trên đường thẳng.
- Dùng sợi dây căng thẳng qua 2 điểm F và K để xác định điểm C trên mặt đất (3 điểm F, K, C thẳng hàng).
b) ΔABC có AB // KD (D ∈ BC, K ∈ AC)
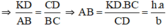
Vậy chiều cao bức tường là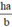 
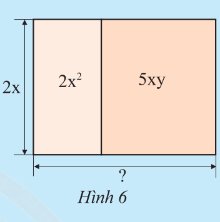
a) Chiều rộng của tấm giấy thứ nhất là: \(2{x^2}:\left( {2x} \right) = \left( {2:2} \right).\left( {{x^2}:x} \right) = x\) (m)
Chiều rộng tấm giấy thứ hai là: \(5xy:\left( {2x} \right) = \left( {5:2} \right).\left( {x:x} \right).y = \frac{5}{2}y\) (m)
Chiều rộng của bức tường là: \(x + \frac{5}{2}y\) (m)
b) Kết quả của phép chia đa thức \(A = 2{x^2} + 5xy\) cho đa thức \(B = 2x\) là \(x + \frac{5}{2}y\)
Vì \(\left( {x + \frac{5}{2}y} \right).\left( {2x} \right) = x.2x + \frac{5}{2}y.2x = 2{x^2} + 5xy\)