K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
NV
Nguyễn Việt Lâm
Giáo viên
30 tháng 7 2021
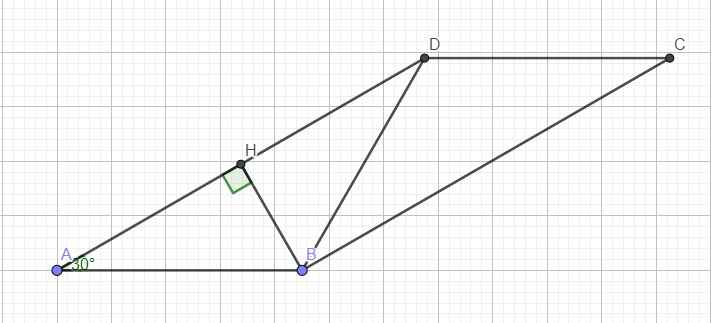
Kẻ đường cao BH ứng với AD
Do \(AB=AD\Rightarrow\Delta ABD\) cân tại B
\(\Rightarrow\) BH là đường cao đồng thời là trung tuyến
\(\Rightarrow AH=HD=\dfrac{1}{2}AD\)
Trong tam giác vuông ABH ta có:
\(sinA=\dfrac{BH}{AB}\Rightarrow BH=AB.sinA=18.sin30^0=9\left(cm\right)\)
\(cosA=\dfrac{AH}{AB}\Rightarrow AH=AB.cosA=18.cos30^0=9\sqrt{3}\left(cm\right)\)
\(\Rightarrow AD=2AH=18\sqrt{3}\left(cm\right)\)
\(S_{ABCD}=BH.AD=162\sqrt{3}\left(cm^2\right)\)
NL
0
B
26 tháng 2 2020
diện tích mảnh đất còn lại:
(30 x 60) x 84 : 100 = 504 ( m2 )
diện tích lối đi:
(30 x 60) - 504 = 600-504 = 96 ( m2 )
vì lối đi có chiều rộng không đổi (túc chiều rộng hình chữ nhật không đổi)nên bề rộng lối đi là
96 : 20 = 4,8 ( m )
Đáp số : ...
Đổi xong bạn ấn F5.