K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
P
Phong
CTVHS
14 tháng 1 2024
Câu 5:
a) Số học sinh nữ của trường Tiểu học đó là:
\(40\%\times850=340\left(hs\right)\)
b) Số học sinh nam của trường Tiểu học là:
\(850-340=510\left(hs\right)\)
Tỉ số phần trăm giữ số học sinh nữ và số học sinh nam là:
\(\left(340\times100\%\right):510=66,67\%\)
Đáp số: ...
Nguyễn Trúc Giang 42 phút trước (15:38)
GV
là số thứ bao nhiêu?
4
GV
5 tháng 7 2017
1 + 2 + 3 + 4 + ... + 29 = 30 x 14 + 15 = 435 phân số cho đến khi mẫu số bằng 29
435 + 15 = 450
Số hạng thứ 450 là
NT
Nguyễn Thị Thương Hoài
Giáo viên
VIP
23 tháng 8
Giải:
Trung bình cộng của 100 số tự nhiên liên tiếp đầu tiên là trung bình cộng của số thứ nhất và số thứ một trăm của dãy số gồm 100 số tự nhiên liên tiếp đầu tiên.
Số thứ tự nhiên thứ nhất là: 0
Số tự nhiên thứ 100 là:
(100 - 1) x 1 + 0 = 99
Trung bình cộng của 100 số tự nhiên liên tiếp đầu tiên là:
(0 + 99): 2 = \(\frac{99}{2}\)
Đáp số: 99/2
AH
Akai Haruma
Giáo viên
26 tháng 1 2024
Bài 221:
Bán kính hình tròn là:
$12,56:2:3,14=2$ (cm)
Diện tích hình tròn là:
$2\times 2\times 3,14=12,56$ (cm2)
AH
Akai Haruma
Giáo viên
26 tháng 1 2024
Bài 219:
a. Bán kính: $15:2=7,5$ (cm)
Diện tích hình tròn: $7,5\times 7,5\times 3,14=176,625$ (cm2)
b. Bán kính: $0,2:2=0,1$ (m)
Diện tích hình tròn: $0,1\times 0,1\times 3,14=0,0314$ (m2)
c. Bán kính: $\frac{2}{5}:2=0,2$ (dm)
Diện tích hình tròn: $0,2\times 0,2\times 3,14=0,1256$ (dm2)
RF
5
27 tháng 2 2021
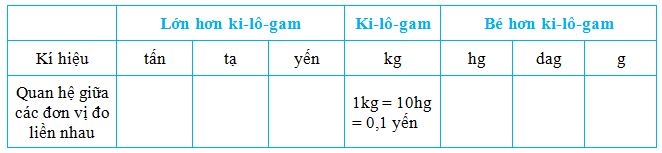
c)
-Đơn vị lớn gấp 10 lần đơn vị bé tiếp liền
-Đơn vị lớn bằng một phần mười đơn vị lớn hơn tiếp liền
6 tháng 6 2023
Vì EC = 1/2 BE nên BE = 2/3 BC và EC = 1/3 BC
a, Chiều rộng hình chữ nhật ABCD là:
12 : 2 = 6 ( cm2 )
Độ dài cạnh BE là:
12 x 2/3 = 8 ( cm2 )
Diện tích hình thang ABED là:
( 12 + 8 ) x 6 : 2 = 60 ( cm2 )
MIK chịu câu B
NV
Nguyễn Việt Lâm
Giáo viên
22 tháng 1 2024
Lượng nước có trong 120kg nấm tươi là:
\(120-90=30\left(kg\right)\)
Phần trăm lượng nước chứa trong nấm là:
\(30:120=25\%\)
14 tháng 9
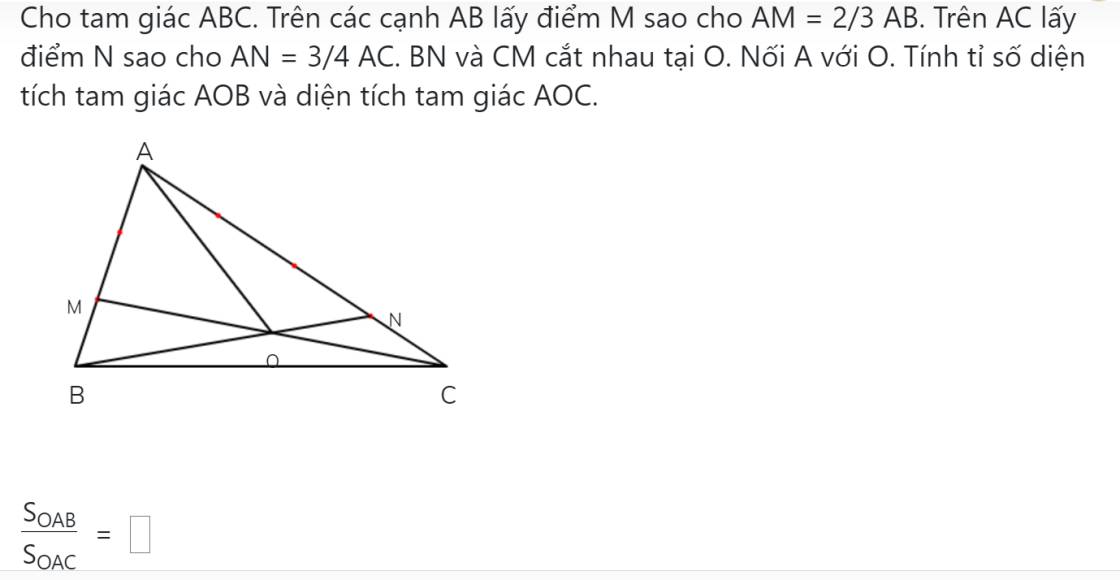
Ta có: AM+MB=AB
=>\(MB=AB-AM=AB-\frac23\times AB=\frac13\times AB\)
=>AM=2xMB
=>\(S_{CMA}=2\times S_{CMB};S_{OMA}=2\times S_{OMB}\)
=>\(S_{CMA}-S_{OMA}=2\times\left(S_{CMB}-S_{OMB}\right)\)
=>\(S_{COA}=2\times S_{COB}\)
Ta có: AN+NC=AC
=>\(NC=AC-AN=AC-\frac34\times AC=\frac14\times AC\)
=>AN=3xNC
=>\(S_{BNA}=3\times S_{BNC};S_{ONA}=3\times S_{ONC}\)
=>\(S_{BNA}-S_{ONA}=3\times\left(S_{BNC}-S_{ONC}\right)\)
=>\(S_{BOA}=3\times S_{BOC}\)
=>\(\frac{S_{AOB}}{S_{AOC}}=\frac{3\times S_{BOC}}{2\times S_{BOC}}=\frac32\)