
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


a) Vì ABCD là hình thoi(gt). Mà AC và BD cắt nhau tại O
=> O là trung điểm của AC và BD (t/c của hình bình hành)
=> OB=OD. Mà BE=DF(gt)
=> OB-BE=OD-DF => OE=OF. Mà O nằm giữa E và F
=> O là trung điểm của EF
Xét tứ giác AECF có: AC cắt EF tại O
Mà O là trung điểm của AC( c/m trên )
O là trung điểm của EF( c/m trên )
=> AECF là hình bình hành (Tứ giác có 2 đ/c cắt nhau tại trung điểm của mỗi đg là hình bình hành)
b) Để AECF là hình thoi => \(AC\perp EF\) tại O
=> \(AC\perp BD\) tại O \(\left(E,F\in\left(O\right)\right)\)
Xét hình bình hành ABCD có: \(AC\perp BD\) tại O (c/m trên)
=> ABCD là hình thoi (Hình bình hành có 2 đ/c vuông góc là hình thoi)
Vậy để AECF là hình thoi thì ABCD là hình thoi
a) Vì ABCD là hình thoi(gt). Mà AC và BD cắt nhau tại O
=> O là trung điểm của AC và BD (t/c của hình bình hành)
=> OB=OD. Mà BE=DF(gt)
=> OB-BE=OD-DF => OE=OF. Mà O nằm giữa E và F
=> O là trung điểm của EF
Xét tứ giác AECF có: AC cắt EF tại O
Mà O là trung điểm của AC( c/m trên )
O là trung điểm của EF( c/m trên )
=> AECF là hình bình hành (Tứ giác có 2 đ/c cắt nhau tại trung điểm của mỗi đg là hình bình hành)
b) Để AECF là hình thoi => AC⊥EFAC⊥EF tại O
=> AC⊥BD tại O (E,F∈(O)
Xét hình bình hành ABCD có: AC⊥BDAC⊥BD tại O (c/m trên)
=> ABCD là hình thoi (Hình bình hành có 2 đ/c vuông góc là hình thoi)
Vậy để AECF là hình thoi thì ABCD là hình thoi

Trong △ OAB, ta có PQ là đường trung bình nên: PQ =1/2 AB (tính chất đường trung bình của tam giác)
Suy ra: 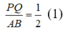 (1)
(1)
Trong △ OAC, ta có PR là đường trung bình nên:
PR = 1/2 AC (tính chất đường trung bình của tam giác)
Suy ra: 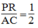 (2)
(2)
Trong △ OBC, ta có QR là đường trung bình nên
QR = 1/2 BC (tính chất đường trung bình của tam giác)
Suy ra: 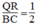
Từ (1), (2) và (3) suy ra: 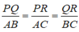
Vậy △ PQR đồng dạng △ ABC (c.c.c)

Trên tia đối của tia MA lấy điểm E sao cho MA=ME
Xét ΔABM và ΔECM có
AM=EM(theo cách vẽ)
\(\widehat{AMB}=\widehat{EMC}\)(hai góc đối đỉnh)
BM=CM(AM là đường trung tuyến ứng với cạnh BC của ΔABC)
Do đó: ΔABM=ΔECM(c-g-c)
⇒AB=CE(hai cạnh tương ứng)
Xét ΔACE có AE<AC+CE(Bất đẳng thức trong tam giác)
mà CE=AB(cmt)
nên AE<AC+AB(1)
Ta có: MA=ME(theo cách vẽ)
mà A,M,E thẳng hàng
nên M là trung điểm của AE
hay \(AE=2\cdot AM\)(2)
Từ (1) và (2) suy ra \(2\cdot AM< AB+AC\)
\(\Leftrightarrow AM< \frac{AB+AC}{2}=\frac{AB}{2}+\frac{AC}{2}\)(3)
Xét ΔABC có
M là trung điểm của BC(AM là đường trung tuyến ứng với cạnh BC của ΔABC)
P là trung điểm của AB(CP là đường trung tuyến ứng với cạnh AB của ΔABC)
Do đó: MP là đường trung bình của ΔABC(Định nghĩa đường trung bình của tam giác)
⇒\(MP=\frac{AC}{2}\)(Định lí 2 về đường trung bình của tam giác)(4)
Xét ΔABC có
M là trung điểm của BC(AM là đường trung tuyến ứng với cạnh BC của ΔABC)
N là trung điểm của AC(BN là đường trung tuyến ứng với cạnh AC của ΔABC)
Do đó: MN là đường trung bình của ΔABC(Định nghĩa đường trung bình của tam giác)
⇒\(MN=\frac{AB}{2}\)(Định lí 2 về đường trung bình của tam giác)(5)
Từ (3), (4) và (5) suy ra MA<MP+MN(đpcm)

1)Điều cần chứng minh : 3 đường trung tuyến của tam giác bất kỳ luôn đồng quy.
Cho tam giác ABC, trung tuyến AM, lấy điểm G trên AM sao cho AG = 2GM, I là trung điểm AG.
BG cắt AC tại N. Qua I, M kẻ các đường thẳng song song với BG cắt AC tại K,L (Bạn tự vẽ hình nhé)
Theo định lý Talét suy ra AK=KN=NL=LC => AN = NC vậy BN là trung tuyến của tam giác ABC
Chứng minh tương tự ta có nếu CG cắt AB tại P thì CP là trung tuyến của tam giác ABC
Vậy 3 trung tuyến của tam giác đồng quy.
2)Phần này đã được chứng minh trong sách giáo khoa 11 trang 44. Trong một số sách tham khảo thì mệnh đề trên được xem như tiên đề.
3) Bạn không nói rõ là công thức cộng thế nào. Nếu là cos(a+b) SGK có chứng minh rồi bạn ạ. Còn nếu là cos x + cos y = 2cos [(x+y)/2]* cos[(x-y)/2] thì nó được suy ra từ công thức nhân khi ta đặt
a+b=x và a-b=y trong công thức nhân. Công thức nhân được chứng minh bằng việc cộng hoặc trừ theo về công thức công cos(a+b) với cos(a-b).
Học toán không chỉ tìm bài toán khó mà suy nghĩ những cái cơ bản cũng cho ta thêm kinh nghiệm, miễn ta yêu thích nó thì không thể nói là phí thời gian được.
Mình có cách khác khá dễ nè:) Boul học hình ghê thật:) tới sin cos rồi á?