K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên

CM
18 tháng 4 2017
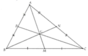
a) Tam giác AGP và PGB có chung đường cao hạ từ đỉnh G và AP = PB nên SAGP = SPGB
Tương tự, ta có: SBGM = SMGC và SCGN = SNGA.
Vì G là trọng tâm DABC Þ AG = 2GM.
Þ SBGM = 1 2 SABG Þ SBGM = SAGP = SPGB.
Chứng minh tương tự, ta suy ra được:
SAGP = SPGB = SBGM = SMGC = SCGN = SNGA
b) Sử dụng kết quả câu a) ta có diện tích mỗi tam giác bằng 1 6 SABC, từ đó suy ra ĐPCM.
Trên tia đối của tia MA lấy điểm E sao cho MA=ME
Xét ΔABM và ΔECM có
AM=EM(theo cách vẽ)
\(\widehat{AMB}=\widehat{EMC}\)(hai góc đối đỉnh)
BM=CM(AM là đường trung tuyến ứng với cạnh BC của ΔABC)
Do đó: ΔABM=ΔECM(c-g-c)
⇒AB=CE(hai cạnh tương ứng)
Xét ΔACE có AE<AC+CE(Bất đẳng thức trong tam giác)
mà CE=AB(cmt)
nên AE<AC+AB(1)
Ta có: MA=ME(theo cách vẽ)
mà A,M,E thẳng hàng
nên M là trung điểm của AE
hay \(AE=2\cdot AM\)(2)
Từ (1) và (2) suy ra \(2\cdot AM< AB+AC\)
\(\Leftrightarrow AM< \frac{AB+AC}{2}=\frac{AB}{2}+\frac{AC}{2}\)(3)
Xét ΔABC có
M là trung điểm của BC(AM là đường trung tuyến ứng với cạnh BC của ΔABC)
P là trung điểm của AB(CP là đường trung tuyến ứng với cạnh AB của ΔABC)
Do đó: MP là đường trung bình của ΔABC(Định nghĩa đường trung bình của tam giác)
⇒\(MP=\frac{AC}{2}\)(Định lí 2 về đường trung bình của tam giác)(4)
Xét ΔABC có
M là trung điểm của BC(AM là đường trung tuyến ứng với cạnh BC của ΔABC)
N là trung điểm của AC(BN là đường trung tuyến ứng với cạnh AC của ΔABC)
Do đó: MN là đường trung bình của ΔABC(Định nghĩa đường trung bình của tam giác)
⇒\(MN=\frac{AB}{2}\)(Định lí 2 về đường trung bình của tam giác)(5)
Từ (3), (4) và (5) suy ra MA<MP+MN(đpcm)
Cảm ơn bạn