
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.






Gọi số viên bi xanh, đỏ, vàng lần lượt là: \(a,b,c\)(viên) \(a,b,c\inℕ^∗\).
Vì tổng số bi là \(35\)viên nên \(a+b+c=35\).
Vì số bi xanh và đỏ tỉ lệ với \(2\)và \(3\)nên \(\frac{a}{2}=\frac{b}{3}\Leftrightarrow\frac{a}{8}=\frac{b}{12}\).
Vì số bi đỏ và vàng tỉ lệ với \(4\)và \(5\)nên \(\frac{b}{4}=\frac{c}{5}\Leftrightarrow\frac{b}{12}=\frac{c}{15}\).
Suy ra \(\frac{a}{8}=\frac{b}{12}=\frac{c}{15}\).
Áp dụng tính chất dãy tỉ số bằng nhau ta có:
\(\frac{a}{8}=\frac{b}{12}=\frac{c}{15}=\frac{a+b+c}{8+12+15}=\frac{35}{35}=1\)
\(\Leftrightarrow\hept{\begin{cases}a=1.8=8\\b=1.12=12\\c=1.15=15\end{cases}}\)



\(\frac{5}{7}.\left(-\frac{3}{11}\right)+\frac{5}{7}.\left(-\frac{8}{11}\right)+2\frac{5}{7}\)
\(=\frac{5}{7}\left(-\frac{3}{11}-\frac{8}{11}+2\right)\)
\(=\frac{5}{7}\left(-\frac{11}{11}+2\right)\)
\(=\frac{5}{7}\left(-1+2\right)\)
\(=\frac{5}{7}.1\)
\(=\frac{5}{7}\)

a) \(\frac{1985.1987-1}{1980+1985.1986}=\frac{1985.1986+1985-1}{1980+1985.1986}=\frac{1985.1986+1984}{1985.1986+1980}>\frac{1985.1986+1980}{1985.1986+1980}=1\)
b) \(A=\frac{13^{15}+1}{13^{16}+1}=\frac{13^{15}+\frac{1}{13}+\frac{12}{13}}{13^{16}+1}=\frac{\frac{1}{13}\left(13^{16}+1\right)+\frac{12}{13}}{13^{16}+1}=\frac{1}{13}+\frac{12}{13\left(13^{16}+1\right)}\)
\(B=\frac{13^{16}+1}{13^{17}+1}=\frac{13^{16}+\frac{1}{13}+\frac{12}{13}}{13^{17}+1}=\frac{\frac{1}{13}\left(13^{17}+1\right)+\frac{12}{13}}{13^{17}+1}=\frac{1}{13}+\frac{12}{13\left(13^{17}+1\right)}\)
Có \(13^{16}+1< 13^{17}+1\)nên \(\frac{12}{13\left(13^{16}+1\right)}>\frac{12}{13\left(13^{17}+1\right)}\)
Vậy \(A>B\).
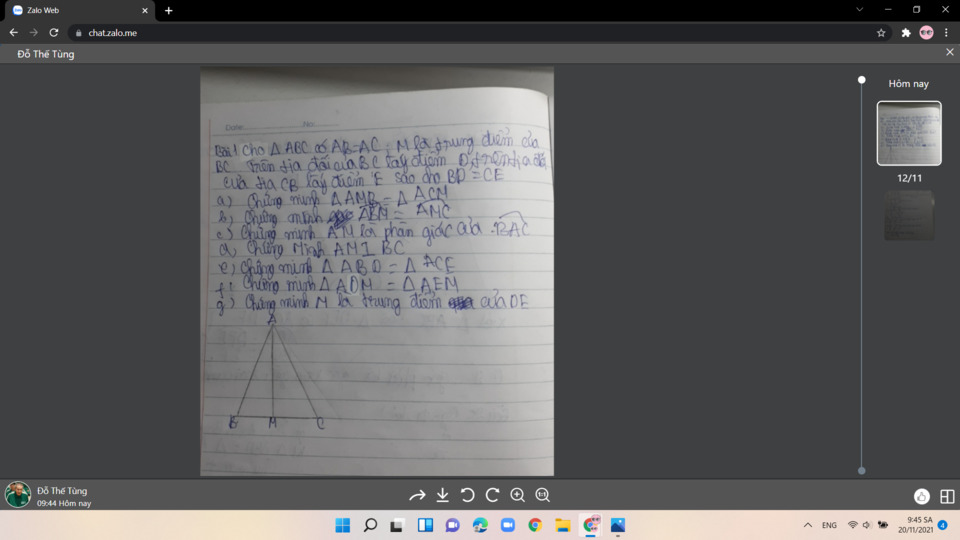

 các bạn giúp mình với mình đang cần gấp
các bạn giúp mình với mình đang cần gấp giúp mình câu này với mình đang cần gấp
giúp mình câu này với mình đang cần gấp





