Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

(a) phân giác trong y=-2 , phân giác ngoài x=2
(b) x=5
(c)x+15y+28=0

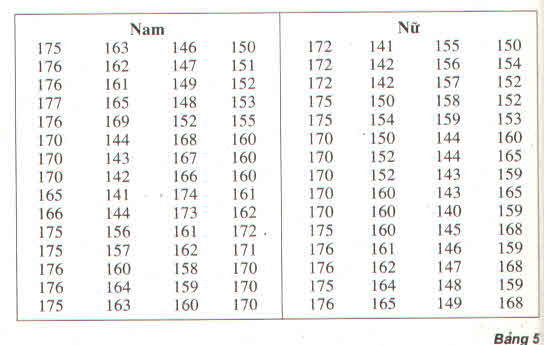
a) Dãy các số liệu chiều cao của các học sinh nam ở bảng 5 có :
\(\overline{x_1}\approx163\left(cm\right);s_1^2\approx134,3;s_1\approx11,59\)
Dãy các số liệu chiều cao của các học sinh nữ cho ở bảng 5 có :
\(\overline{x_2}\approx159,5\left(cm\right);s_2^2\approx148;s_2\approx12,17\)
b) Nhóm T có \(\overline{x_3}=163\left(cm\right);s_3^2=169;s_3=13\)
Học sinh ở nhóm nam và nhóm T có chiều cao như nhau và cùng lớn hơn chiều cao của học sinh ở nhóm nữ (vì \(\overline{x}_1=\overline{x}_3>\overline{x}_2\)
Vì \(\overline{x}_1=\overline{x}_3=163\left(cm\right)\) và \(s_1< s_3\) nên chiều cao của các học sinh nam đồng đều hơn chiều cao của các học sinh nhóm T

Do mình chờ duyệt lâu quá nên các bạn thông cảm giả được báo cho mình
A PHONES
tables chopsiks wardrobes bed fridges dishes desks house rooms lamps posters shinks toilets qpartments laptops buildings books clocks |
/s/ | /is | /z/ |
| |

B A K H C E I D
Ta có \(\widehat{AHC}=\widehat{AEC}=90^0\) nên 4 điểm A, H, C, E cùng thuộc đường tròn đường kính AC.
Gọi I là giao điểm của AC và BD
Ta có \(\widehat{HIE}=2\widehat{HAE}=2\left(180^0-\widehat{BCD}\right)\)
Các tứ giác AKED, AKHB nội tiếp nên \(\widehat{EKD}=\widehat{EAD}\) và \(\widehat{BKH}=\widehat{BAH}\)
Do đó \(\widehat{HKE}=180^0-\widehat{AKD}-\overrightarrow{BKH}=180^0-\overrightarrow{EAD}-\overrightarrow{BAH}=2\overrightarrow{HAE}=2\left(180^0-\overrightarrow{BCD}\right)=\overrightarrow{HIE}\)
Vậy tứ giác HKIE nội tiếp. Do đó I thuộc đường tròn (C) ngoại tiếp tam giác HKE
- Gọi \(C\left(c;c-3\right)\in d\left(c>0\right)\Rightarrow I\left(\frac{c-2}{2};\frac{c-4}{2}\right)\)
Do I thuộc (C) nên có phương trình :
\(c^2-c-2=0\Leftrightarrow c=2\) V c=-1 (loại c=-1) Suy ra \(C\left(2;-1\right);I\left(0;-1\right)\)
- Điểm E, H nằm trên đường tròn đường kính AC và đường tròn (C) nên tọa độ thỏa mãn hệ phương trình :
\(\begin{cases}x^2+y^2+x+4y+3=0\\x^2+\left(y+1\right)^2=4\end{cases}\) \(\Leftrightarrow\begin{cases}x=0;y=-3\\x=-\frac{8}{5};y=-\frac{11}{2}\end{cases}\)
- Vì H có hoành độ âm nên \(H\left(-\frac{8}{5};-\frac{11}{5}\right);E\left(0;-3\right)\) Suy ra \(AB:x-y+1=0;BC:x-3y-5=0\)
Tọa độ B thỏa mãn \(\begin{cases}x-y+1=0\\x-3y-5=0\end{cases}\) \(\Leftrightarrow B\left(-4;-3\right)\Rightarrow\overrightarrow{BA}=\left(2;2\right);\overrightarrow{BC}=\left(6;2\right)\Rightarrow\overrightarrow{BA}.\overrightarrow{BC}=16>0\)
Vì \(\overrightarrow{AB}=\overrightarrow{DC}\Rightarrow D\left(4;1\right)\)
Vậy \(B\left(-4;-3\right);C\left(2;-1\right);D\left(4;1\right)\)

a) (E) có tiêu điểm \({F_1}\left( { - \sqrt 3 ;0} \right)\) nên \(c = \sqrt 3\).
Phương trình chính tăc của (E) có dạng
\({{{x^2}} \over {{a^2}}} + {{{y^2}} \over {{b^2}}} = 1\)
Ta có: \(M\left( {1;{{\sqrt 3 } \over 2}} \right) \in (E)\)
\(\Rightarrow {1 \over {{a^2}}} + {3 \over {4{b^2}}} = 1\ (1)\)
Và \({a^2} = {b^2} + {c^2} = {b^2} + 3\)
Thay vào (1) ta được :
\(\eqalign{ & {1 \over {{b^2} + 3}} + {3 \over {4{b^2}}} = 1 \cr & \Leftrightarrow 4{b^2} + 3{b^2} + 9 = 4{b^2}(b + 3) \cr}\)
\(\Leftrightarrow 4{b^4} + 5{b^2} - 9 = 0 \Leftrightarrow {b^2} = 1\)
Suy ra \({a^2} = 4\)
Ta có a = 2 ; b = 1.
Vậy (E) có bốn đỉnh là : (-2 ; 0), (2 ; 0)
(0 ; -1) và (0 ; 1).
b) Phương trình chính tắc của (E) là :
\({{{x^2}} \over 4} + {{{y^2}} \over 1} = 1\)
c) (E) có tiêu điểm thứ hai là điểm \(\left( {\sqrt 3 ;0} \right)\). Đường thẳng \(\Delta\) đi qua điểm\(\left( {\sqrt 3 ;0} \right)\) và vuông góc với Ox có phương trình \(x = \sqrt 3\).
Phương trình tung độ giao điểm của \(\Delta\) và \((E)\) là :
\({3 \over 4} + {{{y^2}} \over 1} = 1 \Leftrightarrow {y^2} = \pm {1 \over 2}\)
Suy ra tọa độ của C và D là :
\(C\left( {\sqrt 3 ; - {1 \over 2}} \right)\) và \(\left( {\sqrt 3 ;{1 \over 2}} \right)\)
Vậy CD = 1.