Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
tính hết tất cả các góc dùm mình chỉ được dùng t/c 2 góc đối đỉnh và kiến thức lớp 6 thôi hơi khó tí 😭 mong các bạn làm nhanh lên dùm mình mình sẽ tick cho😊😊😊😊😊
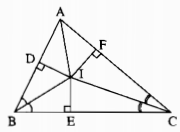
Kẻ: ID⊥AB,IE⊥BC,IF⊥ACID⊥AB,IE⊥BC,IF⊥AC
Xét hai tam giác vuông IDB và IEB, ta có:
\(\eqalign{
& \widehat {I{\rm{D}}B} = \widehat {IEB} = 90^\circ \cr
& \widehat {DBI} = \widehat {EBI}\left( {gt} \right) \cr} \)
BI cạnh huyền chung
⇒⇒ ∆IDB = ∆IEB (cạnh huyền, góc nhọn)
Suy ra: ID = IE (hai cạnh tương ứng)
Quảng cáo
Xét hai tam giác vuông IEC và IFC, ta có ;
\(\eqalign{
& \widehat {IEC} = \widehat {IFC} = 90^\circ \cr
& \widehat {ECI} = \widehat {FCI}\left( {gt} \right) \cr} \)
CI canh huyền chung
Suy ra: ∆ IEC = ∆IFC (cạnh huyền, góc nhọn)
Suy ra: IE = IF (hai cạnh tương ứng) (2)
Từ (1) và (2) suy ra: ID = IF
Xét hai tam giác vuông IDA và IFA, ta có:
ˆIDA=ˆIFA=90∘IDA^=IFA^=90∘
ID = IF (chứng minh trên)
AI cạnh huyền chung
Suy ra: ∆IDA = ∆IFA (cạnh huyền, cạnh góc vuông)
Suy ra: ˆDAI=ˆFAIDAI^=FAI^ (hai góc tương ứng)
Vậy AI là tia phân giác của ˆA
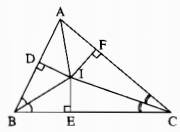
Kẻ: ID⊥AB,IE⊥BC,IF⊥ACID⊥AB,IE⊥BC,IF⊥AC
Xét hai tam giác vuông IDB và IEB, ta có:
ˆIDB=ˆIEB=90∘ˆDBI=ˆEBI(gt)IDB^=IEB^=90∘DBI^=EBI^(gt)
BI cạnh huyền chung
⇒⇒ ∆IDB = ∆IEB (cạnh huyền, góc nhọn)
Suy ra: ID = IE (hai cạnh tương ứng) (1)
Xét hai tam giác vuông IEC và IFC, ta có ;
ˆIEC=ˆIFC=90∘ˆECI=ˆFCI(gt)IEC^=IFC^=90∘ECI^=FCI^(gt)
CI canh huyền chung
Suy ra: ∆ IEC = ∆IFC (cạnh huyền, góc nhọn)
Suy ra: IE = IF (hai cạnh tương ứng) (2)
Từ (1) và (2) suy ra: ID = IF
Xét hai tam giác vuông IDA và IFA, ta có:
ˆIDA=ˆIFA=90∘IDA^=IFA^=90∘
ID = IF (chứng minh trên)
AI cạnh huyền chung
Suy ra: ∆IDA = ∆IFA (cạnh huyền, cạnh góc vuông)
Suy ra: ˆDAI=ˆFAIDAI^=FAI^ (hai góc tương ứng)
Vậy AI là tia phân giác của ˆA
Read more: https://sachbaitap.com/cau-100-trang-151-sach-bai-tap-sbt-toan-lop-7-tap-1-c7a10140.html#ixzz6DFwdbF2W
Diện Tích HTG là
4 x 6 : 2 = 12 (cm2)
Độ dài chiều cao AH là
12 : 6 = 2 (cm2)
xét tam giác ABH và tam giác ACH có : (tam giác vuông)
AH chung
Góc B= Góc C (tam giác cân)
\(\Rightarrow\)tam giác ABH = tam giác ACH (cạnh huyền góc nhọn) \(\Rightarrow\)CH=BH=3 cm
Theo định lý py-ta-go ta có:
Xét tam giác ABH : \(^{AH^2=AB^2-HB^2=4^2-3^2=7}\)
\(\Rightarrow\)\(AH^{ }=\sqrt{7}\)
Không giải đc vì bài toán thiếu dữ kiện. Điểm M nằm ở bất kỳ vị trí nào trong tgABC
Đặt \(A=1+\frac{1}{2}+\frac{1}{2^2}+...+\frac{1}{2^{20}}\)
\(\Rightarrow2A=2+1+\frac{1}{2}+...+\frac{1}{2^9}\)
\(\Rightarrow2A-A=\left(2+1+\frac{1}{2}+...+\frac{1}{2^9}\right)-\left(1+\frac{1}{2}+\frac{1}{2^2}+...+\frac{1}{2^{10}}\right)\)
\(\Rightarrow A=2-\frac{1}{2^{10}}\)
đặt \(A=1+\frac{1}{2}+\frac{1}{2^2}+...+\frac{1}{2^{10}}\)
\(2A=2+1+\frac{1}{2}+...+\frac{1}{2^9}\)
\(2A-A=\left(2+1+\frac{1}{2}+...+\frac{1}{2^9}\right)-\left(1+\frac{1}{2}+\frac{1}{2^2}+...+\frac{1}{2^{10}}\right)\)
\(A=2-\frac{1}{2^{10}}\)
Mong các bạn và thầy cô giáo trên hoc24h giúp mk giả bài 3,4,5,6 trong đề. Cảm ơn mn nhé! 😊😀😁
BT3:
A B C O M
a) Xét \(\widehat{A}+\widehat{B}+\widehat{C}=180^0\) ( định lí tổng ba góc trong một tam giác )
\(\Rightarrow\)\(\widehat{A}+60^0+\widehat{C}=180^0\)
\(\Rightarrow\)\(\widehat{A}+\widehat{C}=120^0\)
\(\Rightarrow2\widehat{OAC}+2\widehat{OCA}=120^0\)
\(\Rightarrow2\left(\widehat{OAC}+\widehat{OCA}\right)\)= 1200
\(\Rightarrow\widehat{OAC}+\widehat{OCA}=60^0\)
Xét \(\widehat{OAC}+\widehat{OCA}+\widehat{AOC}=180^0\) ( định lí tổng ba góc trong một tam giác )
\(\Rightarrow\widehat{AOC}=120^0\)
b) Có tia AO cắt BC tại M
\(\Rightarrow\widehat{BMC}=180^0\)
Lại có: \(\widehat{A}+\widehat{C}=120^0\) ( ở câu a)
\(\Rightarrow\widehat{C}< 120^0< 180^0\)
\(\Rightarrow\widehat{C}< \widehat{BMC}\)
BT3:
A B C H D
a) Xét \(\widehat{A}+\widehat{B}+\widehat{C}=180^0\) (đlí tồng ba góc trong một tam giác )
\(\Rightarrow\widehat{C}=30^0\)
b) Có AD là phân giác góc A
\(\Rightarrow\widehat{CAD}=\widehat{DAB}=\dfrac{90^0}{2}=45^0\)
Xét \(\Delta HAB\) có \(\widehat{H}+\widehat{HAB}+\widehat{HBA}=180^0\) (đlí tồng ba góc trong một tam giác )
\(\Rightarrow\widehat{HAB}=180^0-90^0-60^0=30^0\)
Lại có: \(\widehat{CAD}+\widehat{DAH}+\widehat{HAB}=\widehat{A}=90^0\)
\(\Rightarrow45^0+30^0+\widehat{HAD}=90^0\)
\(\Rightarrow\widehat{HAD}=15^0\)
Nhàn Lê
Ta có :
5,625 = 25,125
TỪ đó ta lập được các tỉ thức sau :
\(\frac{5}{25}=\frac{25}{625}\) ; \(\frac{5}{25}=\frac{25}{625}\);\(\frac{625}{25}=\frac{25}{5}\);\(\frac{625}{25}=\frac{25}{5}\)