
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


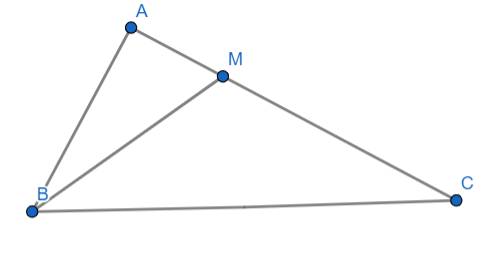
a) Áp dụng định lý Py-ta-go cho tam giác ABC vuông tại A ta có:
\(BC^2=AB^2+AC^2\)
\(\Rightarrow BC=\sqrt{AB^2+AC^2}\)
\(\Rightarrow BC=\sqrt{10^2+20^2}=10\sqrt{5}\left(cm\right)\)
Áp dụng định lý Py-ta-go cho tam giác ABM vuông tại A ta có:
\(BM^2=AB^2+AM^2\)
\(\Rightarrow BM=\sqrt{AB^2+AM^2}\)
\(\Rightarrow BM=\sqrt{10^2+5^2}=5\sqrt{5}\left(cm\right)\)
b) Ta có:
\(\dfrac{AM}{AB}=\dfrac{1}{2}\)
\(\dfrac{BM}{BC}=\dfrac{1}{2}\)
\(\Rightarrow\dfrac{AM}{AB}=\dfrac{MB}{BC}=\dfrac{1}{2}\)
Xét hai tam giác ABC và AMB có:
\(\widehat{BAC}\) chung
\(\dfrac{AM}{AB}=\dfrac{MB}{BC}=\dfrac{1}{2}\)
\(\Rightarrow\Delta ABC\sim\Delta AMB\left(c.g.c\right)\)

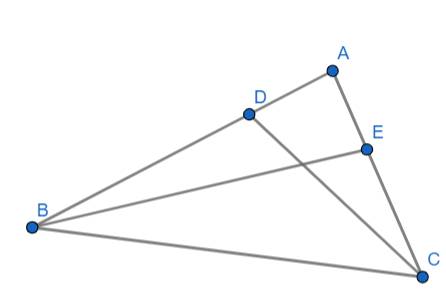
a) Xét hai tam giác ABE và ACD có:
\(\widehat{ACD}=\widehat{ABE}\left(gt\right)\)
\(\widehat{BAC}\) chung
\(\Rightarrow\Delta ABE\sim\Delta ACD\left(g.g\right)\)
b) Ta có: \(\Delta ABE\sim\Delta ACD\left(cmt\right)\)
\(\Rightarrow\dfrac{AB}{AC}=\dfrac{AE}{AD}\)


a) 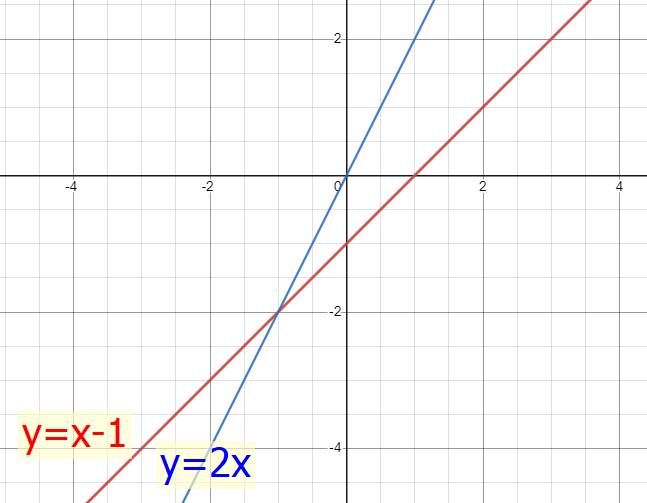
b) Phương trình hoành độ giao điểm của hai đường thẳng là:
\(x-1=2x\)
\(\Leftrightarrow2x-x=-1\)
\(\Leftrightarrow x=-1\)
Thay x = - 1 vào y = 2x ta có: \(y=2\cdot-1=-2\)
Vậy tọa độ giao điểm của 2 đường thẳng là \(\left(-1;-2\right)\)

a) Vào năm 2000 diện tích đất nông nghiệp ở nước ta là:
Thay t = 0 vào \(S=0,12t+8,97\) (vì t được tính theo số năm kể từ năm 2000) ta có:
\(S=0,12\cdot0+8,97=8,97\left(tr.ha\right)\)
b) Diện tích đất nông nghiệp ở nước ra đạt 10,05 triệu hec-ta ta thay \(S=10,05\) ta có:
\(10,05=0,12t+8,97\)
\(\Leftrightarrow0,12t=10,05-8,97\)
\(\Leftrightarrow0,12t=1,08\)
\(\Leftrightarrow t=1,08:0,12\)
\(\Leftrightarrow t=9\)
Vậy năm nước ta đạt 10,05 triệu héc-ta là: \(2000+9=2009\)

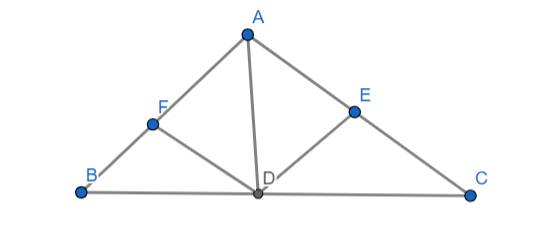
a) Ta có:
\(DF//AC\left(gt\right)\) (1)
\(DE//AB\left(gt\right)\) (2)
Từ (1) và (2) ⇒ AEDF là hình bình hành (3)
Mà AD là phân giác của góc FAE (4)
Từ (3) và (4) ⇒ AEDF là hình thoi
b) Xét hai tam giác CDE và CBA có:
\(\widehat{ACB}\) chung
\(\widehat{CED}=\widehat{CAB}\) (đồng vị vì DE//AB)
\(\Rightarrow\Delta CDE\sim\Delta CBA\left(g.g\right)\)
\(\Rightarrow\dfrac{DE}{AB}=\dfrac{CE}{AC}\Rightarrow DE\cdot AC=CE\cdot AB\)
Do: AEDF là hình thoi nên: DE = AE = AF
\(\Rightarrow AF\cdot AC=\left(AC-AE\right)\cdot AB\)
\(\Rightarrow\left(AB-BF\right)\cdot AC=AC\cdot AB-AE\cdot AB\)
\(\Rightarrow AB\cdot AC-BF\cdot AC=AC\cdot AB-AE\cdot AB\)
\(\Rightarrow BF\cdot AC=AE\cdot AB\)
\(\Rightarrow AF\cdot AB=BF\cdot AC\left(đpcm\right)\)



Ta có: DE//AC (cùng vuông góc với AB)
Áp dụng định lý Ta-lét ta có:
\(\dfrac{BD}{AD}=\dfrac{BE}{CE}\Rightarrow\dfrac{BD}{AD}=\dfrac{BE}{BC-BE}\Rightarrow\dfrac{6}{x}=\dfrac{3x}{13,5-3x}\)
\(\Leftrightarrow6\left(13,5-3x\right)=x\cdot3x\)
\(\Leftrightarrow81-18x=3x^2\)
\(\Leftrightarrow27-6x=x^2\)
\(\Leftrightarrow x^2+6x-27=0\)
\(\Leftrightarrow x^2-3x+9x-27=0\)
\(\Leftrightarrow x\left(x-3\right)+9\left(x-3\right)=0\)
\(\Leftrightarrow\left(x-3\right)\left(x+9\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x=3\left(tm\right)\\x=-9\left(ktm\right)\end{matrix}\right.\)
Vậy: `x=3`
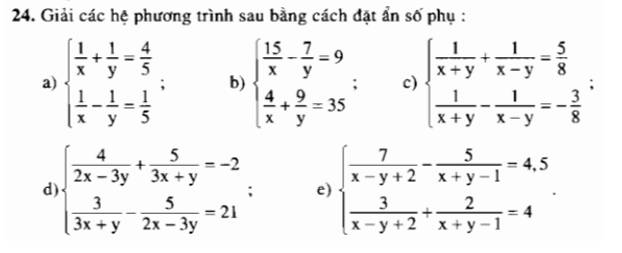
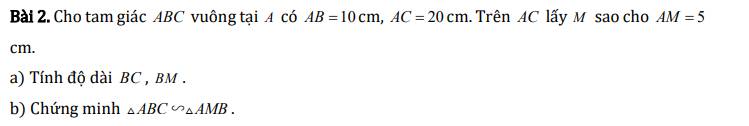
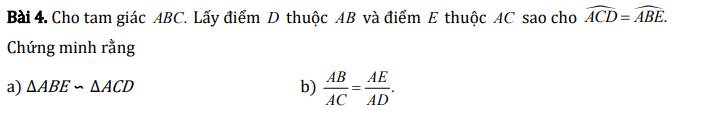






 Trả lời lẹ giúp em đi ạ
Trả lời lẹ giúp em đi ạ
a:
ĐKXĐ: \(x\ne0;y\ne0\)
Đặt \(\dfrac{1}{x}=a;\dfrac{1}{y}=b\)
Hệ phương trình sẽ trở thành \(\left\{{}\begin{matrix}a+b=\dfrac{4}{5}\\a-b=\dfrac{1}{5}\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}2a=1\\a-b=\dfrac{1}{5}\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}a=\dfrac{1}{2}\\b=a-\dfrac{1}{5}=\dfrac{1}{2}-\dfrac{1}{5}=\dfrac{3}{10}\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}\dfrac{1}{x}=\dfrac{1}{2}\\\dfrac{1}{y}=\dfrac{3}{10}\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=2\\y=\dfrac{10}{3}\end{matrix}\right.\left(nhận\right)\)
b: ĐKXĐ: \(x\ne0;y\ne0\)
Đặt \(\dfrac{1}{x}=a;\dfrac{1}{y}=b\)
Hệ phương trình sẽ trở thành:
\(\left\{{}\begin{matrix}15a-7b=9\\4a+9b=35\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}60a-28b=36\\60a+135b=140\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}-163b=-104\\4a+9b=35\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}b=\dfrac{104}{163}\\a=\dfrac{4769}{652}\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}\dfrac{1}{x}=\dfrac{4769}{652}\\\dfrac{1}{y}=\dfrac{104}{163}\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=\dfrac{652}{4769}\\y=\dfrac{163}{104}\end{matrix}\right.\)(nhận)
c: ĐKXĐ: \(x\ne\pm y\)
Đặt \(\dfrac{1}{x+y}=a;\dfrac{1}{x-y}=b\)
Hệ phương trình sẽ trở thành:
\(\left\{{}\begin{matrix}a+b=\dfrac{5}{8}\\a-b=-\dfrac{3}{8}\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}2a=\dfrac{5}{8}-\dfrac{3}{8}=\dfrac{2}{8}=\dfrac{1}{4}\\a+b=\dfrac{5}{8}\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}a=\dfrac{1}{4}\\b=\dfrac{5}{8}-\dfrac{1}{4}=\dfrac{3}{8}\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}\dfrac{1}{x+y}=\dfrac{1}{4}\\\dfrac{1}{x-y}=\dfrac{3}{8}\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x+y=4\\x-y=\dfrac{8}{3}\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}2x=4+\dfrac{8}{3}=\dfrac{20}{3}\\x+y=4\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}x=\dfrac{10}{3}\\y=4-x=4-\dfrac{10}{3}=\dfrac{2}{3}\end{matrix}\right.\left(nhận\right)\)
d: ĐKXĐ: \(y\ne-3x;y\ne\dfrac{2}{3}x\)
Đặt \(\dfrac{1}{2x-3y}=a;\dfrac{1}{3x+y}=b\)
Hệ phương trình sẽ trở thành:
\(\left\{{}\begin{matrix}4a+5b=-2\\-5a+3b=21\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}20a+25b=-10\\-20a+12b=84\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}37b=84-10=74\\4a+5b=-2\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}b=2\\a=-3\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}\dfrac{1}{2x-3y}=-3\\\dfrac{1}{3x+y}=2\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}2x-3y=-\dfrac{1}{3}\\3x+y=\dfrac{1}{2}\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}2x-3y=-\dfrac{1}{3}\\9x+3y=\dfrac{3}{2}\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}11x=-\dfrac{1}{3}+\dfrac{3}{2}=\dfrac{7}{6}\\y=\dfrac{1}{2}-3x\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}x=\dfrac{7}{66}\\y=\dfrac{1}{2}-3\cdot\dfrac{7}{66}=\dfrac{1}{2}-\dfrac{7}{22}=\dfrac{4}{22}=\dfrac{2}{11}\end{matrix}\right.\)
e: ĐKXĐ:\(x\ne y-2;x\ne-y+1\)
Đặt x-y+2=a; x+y-1=b
Hệ phương trình sẽ trở thành:
\(\left\{{}\begin{matrix}\dfrac{7}{a}-\dfrac{5}{b}=4,5\\\dfrac{3}{a}+\dfrac{2}{b}=4\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}\dfrac{14}{a}-\dfrac{10}{b}=9\\\dfrac{15}{a}+\dfrac{10}{b}=20\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}\dfrac{29}{a}=29\\\dfrac{3}{a}+\dfrac{2}{b}=4\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}a=1\\\dfrac{2}{b}=4-\dfrac{3}{a}=4-3=1\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}a=1\\b=2\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}x-y+2=1\\x+y-1=2\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x-y=-1\\x+y=3\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=1\\y=2\end{matrix}\right.\)(nhận)