
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


A) để lập số có 3 chữ số khác nhau thì:
- có 7 cách chọn chữ số hàng trăm
- Sau khi chọn chữ số hàng trăm, sẽ có 6 cách chọn chữ số hàng chục (chữ số hàng chục không trùng với chữ số hàng trăm đã chọn)
- Sau khi chọn chữ số hàng trăm và hàng chục, có 5 cách chọn chữ số hàng đơn vị (chữ số hàng đơn vị không được trùng với chữ số hàng chục và hàng đơn vị đã chọn)
Vậy có 7.6.5 = 210 cách chọn
B) Số các số {abc | a <= b <= c}
a = 7
b = 7, có 7 cách chọn c
b = 6, có 6 cách chọn c
...
b = 1, có 1 cách chọn c
=> Với a = 7, có 7 + 6 + 5 + ... + 1 cách chọn b và c
Tương tự:
Với a = 6, có 6 + 5 + .. + 1 cách chọn b và c
. . .
Với a = 1, có 1 cách chọn b và c
Vậy có tất số cách là:
(7 + 6 + ... + 1) + (6 + 5 + .. + 1) + ... (2 + 1) + 1
= 7.8/2 + 6.7/2 + ... + 2.3/2 + 1.2/2
= (7.8 + 6.7 + ... + 2.3 + 1.2)/2
= ...
tìm giá trị nhỏ nhất và giá trị lớn nhất của các hàm số sau:
a/ y =
#Hỏi cộng đồng OLM
#Toán lớp 11

a) Hàm số f(x) = xác định trên R\{
} và ta có x = 4 ∈ (
;+∞).
Giả sử (xn) là dãy số bất kì và xn ∈ (;+∞); xn ≠ 4 và xn → 4 khi n → +∞.
Ta có lim f(xn) = lim =
=
.
Vậy
=
.
b) Hàm số f(x) = xác định trên R.
Giả sử (xn) là dãy số bất kì và xn → +∞ khi n → +∞.
Ta có lim f(xn) = lim = lim
= -5.
Vậy
= -5.
Một thấu kính hội tụ có tiêu cự là f. Gọi d và d' lần lượt là khoảng cách từ một vật thật AB và từ ảnh A'B' của nó tới quang tâm O của thấu kính (h.54). Công thức thấu kính là 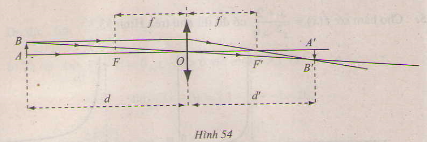
a) Tìm biểu thức xác định hàm số d' = φ(d).
b) Tìm
#Hỏi cộng đồng OLM
#Toán lớp 11

a) Từ hệ thức suy ra d' = φ(d) =
.
b) +) φ(d) =
= +∞ .
Ý nghĩa: Nếu vật thật AB tiến dần về tiêu điểm F sao cho d luôn lớn hơn f thì ảnh của nó dần tới dương vô cực.
+) φ(d) =
= -∞.
Ý nghĩa: Nếu vật thật AB tiến dần về tiêu điểm F sao cho d luôn nhỏ hơn f thì ảnh của nó dần tới âm vô sực.
+) φ(d) =
=
= f.
Ý nghĩa: Nếu vật thật AB ở xa vô cực so với thấu kính thì ảnh của nó ở ngay trên tiêu diện ảnh (mặt phẳng qua tiêu điểm ảnh F' và vuông góc với trục chính).
Cho tam giác ABC. Lấy điểm S nằm ngoài mặt phẳng (ABC). Trên đoạn SA lấy điểm M sao cho
#Hỏi cộng đồng OLM
#Toán lớp 11

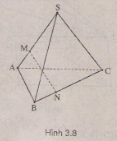
=
+
+
= +
+
(1)
=
+
+
= +
+
(2)
Nhân (2) với 2 rồi cộng với (1) ta được: =
+
Vậy ,
,
đồng phẳng.
 (x4 – x2 + x - 1) =
(x4 – x2 + x - 1) = 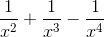 ) = +∞.
) = +∞. (-2x3 + 3x2 -5 ) =
(-2x3 + 3x2 -5 ) = 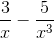 ) = +∞.
) = +∞.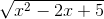 =
= 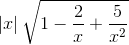 = +∞.
= +∞. =
= 
 =
= 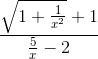 = -1.
= -1.