Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Bài 3:
\(=\left(\dfrac{3}{5}+\dfrac{2}{7}+\dfrac{4}{35}\right)+\left(-\dfrac{1}{2}-\dfrac{1}{9}-\dfrac{7}{18}\right)+\dfrac{1}{131}\)
\(=\dfrac{21+10+4}{35}+\dfrac{-9-2-7}{18}+\dfrac{1}{131}\)
=1/131
Bài 5:
a: Phần nguyên là 0
b: Phần nguyên là -1

a) 2n = 16/2=8= 23 => n =3
b) (-3)n = (-27).81 =(-3)3.34= (-3)7 => n = 7
c) 4 =22= 23n.2n = 23n-n = 22n => n =1

Câu 1:
Các số là STP hữu hạn là -5/64; 7/625; -13/400 vì khi phân tích mẫu của chúng ra thừa số, không có thừa số nào khác 2 và 5
Các số còn lại là STP vô hạn tuần hoàn vì khi phân tích mẫu của chúng ra thừa số nguyên tố, có thừa số khác 2 và 5
Câu 2:
0,(8)=8/9
0,11(7)=53/450
3,(5)=32/9
-17,(23)=-1706/99

a, 1,2 : 3,24 = 120/324 = 10/27
Ta có tỉ lệ thức: 1,2 : 3,24 = 10 : 27
b, 2 và 1/5 : 3/4 = 11/5 : 3/4 = 11/5 . 4/3 = 44/15
Ta có tỉ lệ thức: 2 và 1/5 : 3/4 = 44 : 15
c, 2/7 : 0,42 = 2/7 : 21/50 = 2/7 . 50/21 = 100/147
Ta có tỉ lệ thức: 2/7 : 0,42 = 100 : 147

Bài 1:
Vì \(\dfrac{a}{b}< \dfrac{c}{d}\) nên ad<bc (1)
Xét tích; a.(b+d)=ab+ad (2)
b.(a+c)=ba+bc (3)
Từ (1),(2),(3) suy ra a.(b+d)<b.(a+c) .
Do đó \(\dfrac{a}{b}< \dfrac{a+c}{b+d}\) (4)
Tương tự ta lại có \(\dfrac{a+c}{b+d}< \dfrac{c}{d}\) (5)
Kết hợp (4),(5) => \(\dfrac{a}{b}< \dfrac{a+c}{b+d}< \dfrac{c}{d}\)
hay x<y<z
Bài 2:
a) x là một số hữu tỉ \(\Leftrightarrow\)\(b-15\ne0\Leftrightarrow b\ne15\)
b)x là số hữu tỉ dương\(\Leftrightarrow b-15>0\Leftrightarrow b>15\)
c) x là số hữu tỉ âm \(\Leftrightarrow b-15< 0\Leftrightarrow b< 15\)
Bài 3:
Ta có: \(\left|x-\dfrac{1}{3}\right|\ge0\) (dấu bằng xảy ra \(\Leftrightarrow x=\dfrac{1}{3}\))
=>\(\left|x-\dfrac{1}{3}\right|+\dfrac{1}{4}\ge\dfrac{1}{4}>\dfrac{1}{5}\)
Vậy A\(>\dfrac{1}{5}\)
Bài 4:
M>0 \(\Leftrightarrow x+5;x+9\) cùng dấu.Ta thấy x+5<x+9 nên chỉ có 2 trường hợp
M>0 \(\left[{}\begin{matrix}x+5;x+9\left(duong\right)\\x+5;x+9\left(am\right)\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x+5\ge0\\x+9\ge0\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x\ge-5\\x\ge-9\end{matrix}\right.\)
Bài 5:
Ta dùng phương pháp phản chứng:
Giả sử tồn tại 2 số hữu tỉ x và y thỏa mãn đẳng thức \(\dfrac{1}{x+y}=\dfrac{1}{x}+\dfrac{1}{y}\)
=>\(\dfrac{1}{x+y}=\dfrac{x+y}{x.y}\Leftrightarrow\left(x+y\right)^2=x.y\)
Đẳng thức này không xảy ra vì \(\left(x+y\right)^2>0\) còn x.y <0 ( do x,y là 2 số trái dấu,không đối nhau)
Vậy không tồn tại 2 số hữu tỉ x và y trái dấu ,không đối nhau thỏa mãn đề bài

Bài 1:
Gọi phân số cần tìm là \(\dfrac{x}{18}\)
Theo đề bài đã cho, ta có:
\(\dfrac{-5}{6}< \dfrac{x}{18}< \dfrac{-1}{2}\)
\(\Rightarrow\dfrac{-15}{18}< \dfrac{x}{18}< \dfrac{-9}{18}\)
\(\Rightarrow-15< x< -9\)
\(\Rightarrow x=\left\{-14;-13;-12;-11;-10\right\}\)
Vậy các phân số cần tìm là:
\(\dfrac{-14}{18};\dfrac{-13}{18};\dfrac{-12}{18};\dfrac{-11}{18};\dfrac{-10}{18}\)
Bài 2:
a) Để x là một số hữu tỉ
\(x=\dfrac{5}{a-1}\) \(\in Q\)
\(\Rightarrow a-1\) khác 0
\(\Rightarrow a\) khác 1.
b) Để x là một số dương.
\(x=\dfrac{5}{a-1}\) \(>0\)
\(\Rightarrow a-1>0\)
\(\Rightarrow a>1\)
c) Để x là một số hữu tỉ âm
\(x=\dfrac{5}{a-1}\) <0\(\Rightarrow a-1< 0\)
d) Để x là một số nguyên
\(x=\dfrac{5}{a-1}\) \(\in Z\)
\(\Rightarrow a-1⋮5\)
\(\Rightarrow a-1\inƯ\left(5\right)=\left\{\pm1;\pm5\right\}\)
Ta có bảng sau:
| a-1 | 1 | -1 | 5 | -5 |
| a | 2 | 0 | 6 | -4 |
Vậy a= 2; 0; 6; -4

Bài 1: Giải:
Tổng của 7 số đầu là:
16.7=112
Tổng của 8 số là:
17.8=136
Số thứ 8 là:
136-112=24
Vậy số thứ 8 là: 24
( mik tưởng dạng này học ở cấp 1 chứ?)
Bài 1: Trung bình cộng của bảy số là 16. Do thêm số thứ 8 nên trung bình cộng của tám số là 17. Tìm số thứ tám.
Giải:
Tổng của 7 số là: 16 . 7 = 112
Tổng của 8 số là: 17 . 8 = 136
Số thứ 8 là: 136 - 112 = 24
Vậy số thứ 8 là 24

Xét tích: a(b+2001) = ab + 2001a
b(a+2001) = ab + 2001b. Vì b > 0 nên b + 2001 > 0
*Nếu a > b thì ab + 2001a > ab + 2001b
a(b + 2001) > b(a + 2001)
=> \(\dfrac{a}{b}\) > \(\dfrac{a+2001}{b+2001}\)
*Tương tự nếu a < b thì => \(\dfrac{a}{b}\) < \(\dfrac{a+2001}{b+2001}\)
*Và nếu a = b thì => \(\dfrac{a}{b}\)=\(\dfrac{a+2001}{b+2001}\)
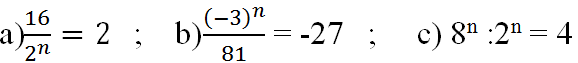
Lời giải:
a)
\(0,(7)=\frac{7}{9}\); \(0,(23)=\frac{23}{99}\)
b) \(1,(7)=1+0,(7)=1+\frac{7}{9}=\frac{16}{9}\)
\(1,(23)=1+0,(23)=1+\frac{23}{99}=\frac{122}{99}\)
c) \(1,2(7)=\frac{12,(7)}{10}=\frac{12+0,(7)}{10}=\frac{12+\frac{7}{9}}{10}=\frac{23}{18}\)
\(1,7(23)=\frac{17,(23)}{10}=\frac{17+0,(23)}{10}=\frac{17+\frac{23}{99}}{10}=\frac{853}{495}\)