
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Công thức tính diện tích hình tam giác :
\(\frac{a\times h}{2}\)
a: Đáy ; h: Chiều cao
Công Thức:
(Chiều cao \(\times\) Đáy) \(\div\) 2 = Diện Tích
Ký hiệu:
a = Đáy
h = Chiều cao
S = Diện tích
\(\text{S}=\left(\text{a}\times\text{h}\right)\div2\)


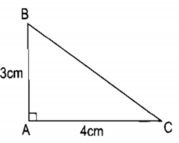
Bài giải
Diện tích hình tam giác đó là :
4 x 3 : 2 = 6 ( cm2 )
Đ/s : 6 cm2 .

HÌNH CHỮ NHẬT
- Chu vi: P = (a + b) x 2 (P: chu vi)
- Diện tích: S = a x b (S: diện tích)
HÌNH VUÔNG:
- Chu vi: P = a x 4 (P: chu vi)
- Diện tích: S = a x a (S: diện tích)
HÌNH TAM GIÁC:
- Chu vi: P = a + b + c (a: cạnh thứ nhất; b: cạnh thứ hai; c: cạnh thứ ba)
- Diện tích: S = (a x h) : 2 (a: cạnh đáy)
- Chiều cao: h = (S x 2) : a (h: chiều cao)
- Cạnh đáy: a = (S x 2) : h
HÌNH BÌNH HÀNH:
- Chu vi: P = (a + b) x 2 (a: độ dài đáy)
- Diện tích: S = a x h (b: cạnh bên)
- Diện tích: S = a x h (h: chiều cao)
- Độ dài đáy: a = S : h
- Chiều cao: h = S : a
- Diện tích: S = (m x n) : 2 (m: đường chéo thứ nhất)
- Tích 2 đường chéo: (m x n) = S x 2 (n: đường chéo thứ nhất)
- HÌNH THANG
- Diện tích: S = (a + b) x h : 2 (a & b: cạnh đáy)
- Chiều cao: h = (S x 2) : a (h: chiều cao)
- Cạnh đáy: a = (S x 2) : h
HÌNH TRÒN:
- Bán kính hình tròn: r = d : 2 hoặc r = C : 2 : 3,14
- Đường kính hình tròn: d = r x 2 hoặc d = C : 3,14
- Chu vi hình tròn: C = r x 2 x 3,14 hoặc C = d x 3,14
- Diện tích hình tròn: C = r x r x 3,14
- Diện tích xung quanh: Sxq = (a x a) x 4
- Cạnh: (a x a) = Sxq : 4
- Diện tích toàn phần: Stp = (a x a) x 6
- Cạnh: (a x a) = Stp : 6
- Diện tích xung quanh: Sxq = Pđáy x h
- Chu vi đáy: Pđáy = Sxq : h
- Chiều cao: h = Pđáy x Sxq

- Khái niệm chu vi hình bình hành : chu vi của một hình bình hành bằng 2 lần tổng một cặp cạnh kề nhau bất kỳ. Nói cách khác, chu vi hình bình là tổng độ dài của 4 cạnh hình bình hành.
còn hình khác bn tự lm nhé
:3

Với bất cứ tam giác nào, diện tích đều bằng một nửa chiều dài đáy nhân với chiều cao tương ứng. Trong một tam giác vuông, nếu một cạnh bên được coi là đáy thì cạnh bên còn lại được xem là chiều cao, diện tích của hình vuông khi đó sẽ bằng một nửa tích giữa hai cạnh bên.
Trong đó a và b là hai cạnh bên của tam giác
Nếu vòng tròn nội tiếp tiếp tuyến cạnh huyền AB tại điểm P, coi bán chu vi (a + b + c) / 2 là s, chúng ta có PA = s − a và PB = s − b
Công thức này chỉ áp dụng với các tam giác vuông.[1]
Theo toán học sơ cấp thì có hai cách tính diện tích tam giác vuông:
- Tích hai cạnh góc vuông tất cả chia hai (Theo tính chất nửa hình chữ nhật)
- Tích cạnh huyền với đường cao (ứng với cạnh huyền) tất cả chia hai (Theo tính chất tam giác)
Chính vì tính chất diện tích này mà có hệ thức đường cao trong tam giác vuông :
bc = ah
Trong đó b và c là hai cạnh góc vuông ; a là cạnh huyền còn h là đường cao ứng với cạnh huyền.


- Công thức tính diện tích tam giác thường: S = (A X H)/ 2
Trong đó:
+ a: Chiều dài đáy tam giác (đáy là một trong 3 cạnh của tam giác tùy theo quy đặt của người tính)
+ h: Chiều cao của tam giác, ứng với phần đáy chiếu lên (chiều cao tam giác bằng đoạn thẳng hạ từ đỉnh xuống đáy, đồng thời vuông góc với đáy của một tam giác).
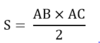
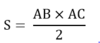
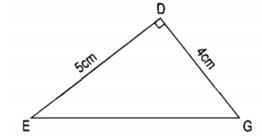
Mỗi loại tam giác sẽ có cách tính khác nhau nhưng với tam giác vuông có lợi thế là dễ xác định chiều cao và có thể tính diện tích tam giác vuông theo công thức sau:
S = a x h : 2
Trong đó;
– S là diện tích
– h là chiều cao
– a là độ dài cạnh đáy