NN
3
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
29 tháng 10 2020
\(x=3+2\sqrt{2}\)
\(x-3-2\sqrt{2}=0\)
\(x-\left(3+2\sqrt{2}\right)=0\) Vậy nhân tử của \(x=3+2\sqrt{2}\) là \(x-\left(3+2\sqrt{2}\right)\)
8 tháng 4 2019
\(x^8-1=\left(x^2-1\right)\left(x^4+x^2+1\right)\)
CÂU SAU THÌ MK KO BIẾT
TT
0
CM
29 tháng 11 2018
3x2 + 8x + 2 = 0
Có a = 3; b' = 4; c = 2
⇒ Δ’ = 42 – 2.3 = 10 > 0
⇒ Phương trình có hai nghiệm phân biệt:
CM
4 tháng 6 2017
* Chứng minh:
Phương trình ax2 + bx + c = 0 có hai nghiệm x1; x2
⇒ Theo định lý Vi-et: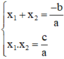 
Khi đó : a.(x – x1).(x – x2)
= a.(x2 – x1.x – x2.x + x1.x2)
= a.x2 – a.x.(x1 + x2) + a.x1.x2
= 
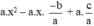
= a.x2 + bx + c (đpcm).
* Áp dụng:
a) 2x2 – 5x + 3 = 0
Có a = 2; b = -5; c = 3
⇒ a + b + c = 2 – 5 + 3 = 0
⇒ Phương trình có hai nghiệm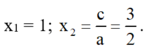 
Vậy: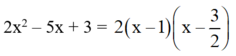 
Q
0
HH
2
DR
21 tháng 7 2015
\(3-\sqrt{3}+\sqrt{6}=\left(\sqrt{3}\right)^2-\sqrt{3}+\sqrt{3}.\sqrt{2}\)
\(=\sqrt{3}.\left(\sqrt{3}-1+\sqrt{2}\right)\)
NP
0
Phân tích nhân tử (hay phân tích ra thừa số nguyên tố) là một thuật ngữ toán học dùng để chỉ một cách viết một số nguyên, hay tổng quát là một vật thể toán học, thành mộtphép nhân của các số nguyên khác, hay tổng quát là các vật thể toán học khác. Các số nguyên, hay vật thể toán học, nằm trong phép nhân gọi là nhân tử nha bạn!!!
k nhé! chúc bạn hok tốt =))
Phân tích nhân tử (hay phân tích ra thừa số nguyên tố) là một thuật ngữ toán học dùng để chỉ một cách viết một số nguyên, hay tổng quát là một vật thể toán học, thành mộtphép nhân của các số nguyên khác, hay tổng quát là các vật thể toán học khác. Các số nguyên, hay vật thể toán học, nằm trong phép nhân gọi là nhân tử nha bạn!!!
((>^,^<))