Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

gọi số phần công việc mỗi đội làm được trong một giờ lần lượt là x và y ( phần / giờ )
Đổi \(\text{ 1 tiếng rưỡi =}\frac{3}{2}\text{ giờ}\)
ta có hệ :
\(\hept{\begin{cases}\frac{1}{x+y}=6\\\frac{1}{2y}-\frac{1}{2x}=\frac{3}{2}\end{cases}\Leftrightarrow\hept{\begin{cases}x+y=6\\x-y=3xy\end{cases}\Rightarrow}\hept{\begin{cases}y=6-x\\x-6+x=3x\left(6-x\right)\end{cases}}}\)
\(\Leftrightarrow\hept{\begin{cases}y=6-x\\3x^2-16x-6=0\end{cases}\Rightarrow\hept{\begin{cases}y=\frac{10-\sqrt{82}}{3}\\x=\frac{8+\sqrt{82}}{3}\end{cases}}}\)vậy đội 1 làm mất \(\frac{3}{8+\sqrt{82}}\text{ giờ}\)
đội 2 làm mất \(\frac{3}{10-\sqrt{82}}\text{ giờ }\)

Gọi số ngày đội một làm riêng để hoàn thành đoạn đường là x (ngày) (x>0)
số ngày đội hai làm riêng để hoàn thành đoạn đường là y (ngày) (y>0)
(x>y)
=> Trong một ngày đội một làm một mình được \(\frac{1}{x}\)(công việc)
Trong một ngày đội hai làm một mình được \(\frac{1}{y}\)(công việc)
Ta có hệ : \(\hept{\begin{cases}\frac{1}{x}+\frac{1}{y}=\frac{1}{48}\\\frac{1}{2}x+\frac{1}{2}y=100\end{cases}}\)
Giải ra được x = 120 ; y = 80 (vì x>y)
Vậy : Nếu làm riêng thì đội một phải làm trong 120 ngày mới xong đoạn đường; đội hai phải làm trong 80 ngày mới xong đoạn đường

Gọi \(x\left(giờ\right),y\left(giờ\right)\) lần lượt là thời gian của đội thứ nhất và đội thứ hai làm riêng xong công việc (x, y > 0)
Trong một giờ hai đội làm được: \(\dfrac{1}{x}+\dfrac{1}{y}=\dfrac{1}{4}\) (công việc)
Đội thứ nhất làm trong 3 giờ rồi đội thứ hai làm tiếp trong 4 giờ được 0,8 công việc nên ta có:
\(\dfrac{3}{x}+\dfrac{4}{y}=0,8\)
Ta có hệ phương trình:
\(\left\{{}\begin{matrix}\dfrac{1}{x}+\dfrac{1}{y}=\dfrac{1}{4}\\\dfrac{3}{x}+\dfrac{4}{y}=0,8\end{matrix}\right.\)
Đặt \(u=\dfrac{1}{x};v=\dfrac{1}{y}\), ta có:
\(\left\{{}\begin{matrix}u+v=\dfrac{1}{4}\\3u+4v=0,8\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}4u+4v=1\\3u+4v=0,8\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}4u+4v=1\\u=\dfrac{1}{5}\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}4.\dfrac{1}{5}+4v=1\\u=\dfrac{1}{5}\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}v=\dfrac{1}{20}\\u=\dfrac{1}{5}\end{matrix}\right.\)
*) \(u=\dfrac{1}{5}\Leftrightarrow\dfrac{1}{x}=\dfrac{1}{5}\Leftrightarrow x=5\) (nhận)
*) \(v=\dfrac{1}{20}\Leftrightarrow\dfrac{1}{y}=\dfrac{1}{20}\Rightarrow y=20\) (nhận)
Vậy đội thứ nhất làm riêng trong 5 giờ xong công việc
đội thứ hai làm riêng trong 20 giờ xong công việc

TK:
1.
Gọi năng xuất làm việc trong 1 ngày của đội 1 và đội 2 lần lượt là:x và y(công việc/ngày).
2 đội công nhân cùng làm chung 1 công việc thì sau 15 ngày
⇒
15
×
y
+
15
×
y
=
1
(
1
)
Đội 1 làm riêng trong 3 ngày rồi dừng lại và đội 2 làm tiếp công việc đó trong 5 ngày thì cả 2 đội hoàn thành 25% công việc(ở đây mk đổi luôn)
⇒
3
×
x
+
5
×
y
=
1
4
⇒
5
×
(
3
×
x
+
5
×
y
)
=
5
×
1
4
15
×
x
+
25
×
y
=
5
4
(
2
)
Lấy (2) trừ đi (1) ta được:
(
15
×
x
+
25
×
y
)
−
(
15
×
x
+
15
×
y
)
=
5
4
−
1
10
×
y
=
1
4
y
=
1
4
:
10
⇒
y
=
1
40
⇒
x
=
1
24
Vậy .................
Tham Khảo:
1.
Gọi năng xuất làm việc trong 1 ngày của đội 1 và đội 2 lần lượt là:x và y(công việc/ngày).
2 đội công nhân cùng làm chung 1 công việc thì sau 15 ngày
⇒15×y+15×y=1(1)⇒15×y+15×y=1(1)
Đội 1 làm riêng trong 3 ngày rồi dừng lại và đội 2 làm tiếp công việc đó trong 5 ngày thì cả 2 đội hoàn thành 25% công việc(ở đây mk đổi luôn)
⇒3×x+5×y=14⇒3×x+5×y=14
⇒5×(3×x+5×y)=5×14⇒5×(3×x+5×y)=5×14
15×x+25×y=54(2)15×x+25×y=54(2)
Lấy (2) trừ đi (1) ta được:
(15×x+25×y)−(15×x+15×y)=54−1(15×x+25×y)−(15×x+15×y)=54−1
10×y=1410×y=14
y=14:10y=14:10
⇒y=140⇒y=140
⇒x=124⇒x=124
Vậy .................

Gọi thời gian mỗi đội làm một mình để xong công việc lần lượt là \(x,y\left(h\right);x,y>0\).
Mỗi giờ mỗi đội làm được lần lượt số phần công việc là: \(\frac{1}{x},\frac{1}{y}\)công việc.
Theo bài ra ta có hệ phương trình:
\(\hept{\begin{cases}4\left(\frac{1}{x}+\frac{1}{y}\right)=1\\3\left(\frac{1}{x}+\frac{1}{y}\right)+\frac{3}{y}=1\end{cases}}\Leftrightarrow\hept{\begin{cases}\frac{1}{x}=\frac{1}{6}\\\frac{1}{y}=\frac{1}{12}\end{cases}}\Leftrightarrow\hept{\begin{cases}x=6\\y=12\end{cases}}\left(tm\right)\).

Gọi thời gian đội 1 làm riêng hết 2/5 công việc là x
=>Thời gian đội 2 hoàn thành công việc là 26-x
Trong 1 ngày đội 1 làm được 2/5*1/x(công việc)
Trong 1 ngày, đội 2 làm được 3/5*1/(26-x)
Theo đề, ta có:
\(\dfrac{2}{5}\cdot\dfrac{1}{x}+\dfrac{3}{5\left(26-x\right)}=\dfrac{1}{12}\)
=>\(\dfrac{2}{5x}+\dfrac{3}{5\left(26-x\right)}=\dfrac{1}{12}\)
=>\(\dfrac{2\left(26-x\right)+3x}{5x\left(26-x\right)}=\dfrac{1}{12}\)
=>130x-5x^2=12(52-2x+3x)
=>-5x^2+130x=12x+624
=>-5x^2+118x-624=0
=>x=78/5(nhận) hoặc x=8(loại)

Gọi x (ngày) là thời gian đội thứ nhất làm riêng xong nửa công việc.
Điều kiện: 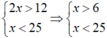 ⇒ 6 < x < 25
⇒ 6 < x < 25
Khi đó thời gian làm riêng xong nửa công việc của đội thứ hai là: 25 – x (ngày)
trong 1 ngày, đội thứ nhất làm được 1/2x (công việc)
trong 1 ngày, đội thứ hai làm được 1/[2.(25 - x)] (công việc)
trong 1 ngày, cả hai đội làm được 1/12 (công việc)
Theo đề bài, ta có phương trình:
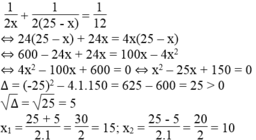
Cả hai giá trị của x đều thỏa mãn điều kiện bài toán
Vậy đội thứ nhất làm riêng xong công việc trong 15.2 = 30 ngày
đội thứ hai làm riêng xong công việc trong 20 ngày
hoặc đội thứ nhất làm riêng xong công việc trong 10.2 = 20 ngày
đội thứ hai làm riêng xong công việc trong 30 ngày.

Gọi thời gian đội 1 và đội 2 hoàn thành công việc một mình lần lượt là x(ngày), y( ngày)(x,y>12)
Mỗi ngày đội 1 làm được phẫn việc là 1/x
Đội 2 làm được số phần việc là 1/y
cả hai đội làm được số phần việc là 1/12
ta có phương trình: 1/x+1/y=1/12(1)
Đội 1 làm trong 5 ngày rồi nghỉ, dội 2 làm tiếp 15 ngày thì họ làm được 75%công việc
từ đó ta có phương trình: 5/x+15/y=3/4(2)
Từ (1)(2) ta có hệ phương trình:{1/x+1/y=1/12; 5/x+15/y=3/4
Giải hệ pt ta tìm được x=20; y=30
KL:Nếu làm một mình thì đội thứ nhất hoàn thành công việc trong 20 ngày, đội thứ hai hoàn thành công việc trong 30 ngày.
