Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Câu 1.
I là trung điểm của AM \(\Rightarrow\overrightarrow{AI}=\frac{1}{2}\overrightarrow{AM}\)
M là trung điểm của BC \(\Rightarrow\) \(\overrightarrow{AM}=\frac{1}{2}\left(\overrightarrow{AB}+\overrightarrow{AC}\right)\)
\(\Rightarrow\overrightarrow{AI}=\frac{1}{4}\left(\overrightarrow{AB}+\overrightarrow{AC}\right)\)
Câu 2.
Ta có: \(2\overrightarrow{MA}+\overrightarrow{MB}=\overrightarrow{CA}\Leftrightarrow2\overrightarrow{MA}+\overrightarrow{MB}=\overrightarrow{MA}-\overrightarrow{MC}\)
\(\Leftrightarrow\overrightarrow{MA}+\overrightarrow{MB}+\overrightarrow{MC}=\overrightarrow{0}\)
\(\Rightarrow\) M là trọng tâm của tam giác ABC.
\(\Rightarrow\) D đúng.
Câu 1:
Theo quy tắc TĐ ta có:
\(\overrightarrow{AM}=\frac{\overrightarrow{AB}+\overrightarrow{AC}}{2}\)
Mà \(\overrightarrow{AI}=\frac{\overrightarrow{AM}}{2}\Rightarrow\overrightarrow{AI}=\frac{\frac{\overrightarrow{AB}+\overrightarrow{AC}}{2}}{2}=\frac{\overrightarrow{AB}+\overrightarrow{AC}}{4}\)
Câu 2:
Có \(\overrightarrow{MA}+\overrightarrow{MB}+\overrightarrow{MA}=\overrightarrow{CA}\Rightarrow\overrightarrow{MC}+\overrightarrow{MB}+\overrightarrow{MA}=0\)
Vậy M là trọng tâm tam giác ABC (D)
Câu 3 sai đề, phải là \(\overrightarrow{BC}=m.\overrightarrow{a}+n.\overrightarrow{b}\) ms đúng chứ?
Câu 4 để mai ik, dài lắm :))

Câu 2:
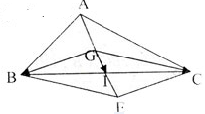
Vì G là trọng tâm nên \(\overrightarrow{GA}+\overrightarrow{GB}+\overrightarrow{GC}=\overrightarrow{0}\)
hay \(\overrightarrow{GC}=-\overrightarrow{a}-\overrightarrow{b}\)
\(\overrightarrow{BC}=\overrightarrow{BG}+\overrightarrow{GC}=-\overrightarrow{b}-\overrightarrow{a}-\overrightarrow{b}=-\overrightarrow{a}-2\overrightarrow{b}\)
=>m=-1; n=-2

Mệnh đề C sai
\(\overrightarrow{GA}+\overrightarrow{GB}=-\overrightarrow{GC}\)
Mà hai vecto \(\overrightarrow{GC}\) và \(\overrightarrow{AM}\) ko cùng phương nên đẳng thức \(\overrightarrow{GA}+\overrightarrow{GB}=\frac{3}{2}\overrightarrow{AM}\) ko thể xảy ra

Theo tính chất trọng tâm ta luôn có:
\(\overrightarrow{GA}+\overrightarrow{GB}+\overrightarrow{GC}=\overrightarrow{0}\)
\(\Leftrightarrow\overrightarrow{GC}=-\overrightarrow{GA}-\overrightarrow{GB}=-\overrightarrow{a}-\overrightarrow{b}\)
\(\Rightarrow m=n=-1\Rightarrow m+n=-2\)

Lời giải:
$G$ là trọng tâm tam giác $ABC$ thì ta có 1 bổ đề quen thuộc là:
$\overrightarrow{GA}+\overrightarrow{GB}+\overrightarrow{GC}=\overrightarrow{0}$
$\Leftrightarrow \overrightarrow{a}+\overrightarrow{b}+\overrightarrow{GC}=\overrightarrow{0}$
$\Rightarrow \overrightarrow{GC}=-(\overrightarrow{a}+\overrightarrow{b})$
Ta có:
\(\frac{1}{2}\overrightarrow{AB}-\overrightarrow{BC}=\frac{1}{2}(\overrightarrow{AG}+\overrightarrow{GB})-(\overrightarrow{BG}+\overrightarrow{GC})\)
\(=\frac{1}{2}(-\overrightarrow{a}+\overrightarrow{b})-[-\overrightarrow{b}-(\overrightarrow{a}+\overrightarrow{b})]\)
\(=\frac{\overrightarrow{a}}{2}+\frac{5\overrightarrow{b}}{2}\)
B